Question

6．如图，在平面直角坐标系中xOy中，边长为10的正方形ABCD的对角线AC，BD相交于点P，点A在x轴正半轴上运动，点B在y轴正半轴上运动（正半轴不包含原点O），点C、D都在第一象限．
（1）当点A坐标为（6，0）时，求点C的坐标；
（2）求证：OP平分∠AOB；
（3）直接写出OP长的取值范围．

Answer 1

分析 （1）过点C作CM⊥y轴于M，△MBC≌△OAB，得到MC=OB，MB=OA，再利用勾股定理求出OB=8，再求出MC，MO的值，即可确定点C的坐标为（8，14）；
（2）过点P作PE⊥y轴于E，过点P作PF⊥x轴于F，则∠BEP=∠AFP=90°，可通过三角形全等，证明OP是角平分线．
（3）因为OP是∠AOB的平分线上，就有∠POA=45°，就有OP=$\sqrt{2}$PF，在Rt△APE中运用三角函数就可以表示出PE的范围，从而可以求出OP的取值范围．．

解答 解：（1）如图1，过点C作CM⊥y轴于M，则∠CMB=∠BOA=90°，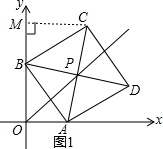

∴∠MBC+∠MCB=90°，
∵四边形ABCD为正方形
∴AB=BC，∠ABC=90°，
∴∠MBC+∠OBA=90°，
∴∠MCB=∠OBA，
在△MBC和△OAB中，
$\left\{\begin{array}{l}{∠MCB=∠OBA}\\{∠CMB=∠BOA}\\{CB=AB}\end{array}\right.$
∴△MBC≌△OAB，
∴MC=OB，MB=OA，
∵点A坐标为（6，0），AB=10
∴$OB=\sqrt{A{B}^{2}-O{A}^{2}}=\sqrt{1{0}^{2}-{6}^{2}}$=8，
∴MC=8，MO=MB+OB=6+8=14，
∴点C的坐标为（8，14）
（2）如图2，过点P作PE⊥y轴于E，过点P作PF⊥x轴于F，则∠BEP=∠AFP=90°，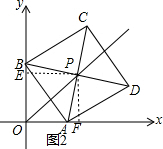

∵∠EOF=90°，
∴∠EPF=90°，即∠EPA+∠APF=90°，
∵四边形ABCD为正方形
∴∠BPA=90°，BP=AP，
∴∠BPA=90°，即∠BPE+∠EPA=90°，
∴∠BPE=∠APF，
在△BPE和△APF中，
$\left\{\begin{array}{l}{∠BEP=∠AFP}\\{∠BPE=∠APF}\\{BP=AP}\end{array}\right.$
∴△BPE≌△APF，
∴PE=PF，
∴OP平分∠AOB．
（3）设∠APF=α．
在直角△APF中，∠AEP=90°，PA=5$\sqrt{2}$．
∴PF=PA•cosα=5$\sqrt{2}$cosa．
∵顶点A在x轴正半轴上运动，顶点B在y轴正半轴上运动（x轴的正半轴、y轴的正半轴都不包含原点O），
∴0°≤α＜45°，
∴$\frac{\sqrt{2}}{2}$＜cosa≤1．
∴5＜PF≤5$\sqrt{2}$，．
∵OP=$\sqrt{2}$PF，
∴5$\sqrt{2}$＜OP≤10
OP长的取值范围为5$\sqrt{2}$＜OP≤10．

点评 本题考查了正方形的性质（四边相等，四角相等，对角线互相垂直平分，且平分每一组对角）以及坐标与图形的性质，全等三角形的判定和性质，解直角三角形，勾股定理的运用，锐角三角函数的运用．