题目内容
12. 定义:有三个内角相等凸四边形叫三等角四边形.
定义:有三个内角相等凸四边形叫三等角四边形.(1)三等角四边形ABCD中,∠A=∠B=∠C,求∠A的取值范围;
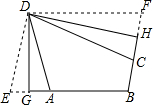
(2)如图,折叠平行四边形纸片DEBF,使顶点E,F分别落在边BE,BF上的点A,C处,折痕分别为DG,DH.求证:四边形ABCD是三等角四边形.
(3)三等角四边形ABCD中,∠A=∠B=∠C<90°,若CB=CD=4,则当AD的长为何值时,AB的长最大,其最大值是多少?(作图解答)
分析 (1)根据四边形的内角和是360°,确定出∠A的范围;
(2)由四边形DEBF为平行四边形,得到∠E=∠F,且∠E+∠EBF=180°,再根据等角的补角相等,判断出∠DAB=∠DCB=∠ABC,即可;
(3)分三种情况分别讨论计算AB的长,从而得出当AD=2时,AB最长;
解答 解:(1)∵∠A=∠B=∠C,
∴3∠A+∠ADC=360°,
∴∠ADC=360°-3∠A.
∵0<∠ADC<180°,
∴0°<360°-3∠A<180°,
∴60°<∠A<120°;
(2)证明:∵四边形DEBF为平行四边形,
∴∠E=∠F,且∠E+∠EBF=180°.
∵DE=DA,DF=DC,
∴∠E=∠DAE=∠F=∠DCF,
∵∠DAE+∠DAB=180°,∠DCF+∠DCB=180°,∠E+∠EBF=180°,
∴∠DAB=∠DCB=∠ABC,
∴四边形ABCD是三等角四边形
(3)①当60°<∠A<90°时,如图1,
过点D作DF∥AB,DE∥BC,
∴四边形BEDF是平行四边形,∠DFC=∠B=∠DEA,
∴EB=DF,DE=FB,
∵∠A=∠B=∠C,∠DFC=∠B=∠DEA,
∴△DAE∽△DCF,AD=DE,DC=DF=4,
设AD=x,AB=y,
∴AE=y-4,CF=4-x,
∵△DAE∽△DCF,
∴$\frac{AE}{CF}$=$\frac{AD}{CD}$,
∴$\frac{y-4}{4-x}$=$\frac{x}{4}$,
∴y=-$\frac{1}{4}$x2+x+4=-$\frac{1}{4}$(x-2)2+5,
∴当x=2时,y的最大值是5,
即:当AD=2时,AB的最大值为5,
②当∠A=90°时,三等角四边形是正方形,
∴AD=AB=CD=4,
③当90°<∠A<120°时,∠D为锐角,如图2,
过点D作DE∥BC,∠DCB=∠CBA,
∴四边形BCDE是等腰梯形,
∴CD=EB=4,
∵AE=4-AB>0,
∴AB<4,
综上所述,当AD=2时,AB的长最大,最大值是5;
点评 此题是四边形综合题,主要考查了四边形的内角和是360°,平行四边形的性质,正方形的性质,相似三角形的性质和判定,勾股定理,解本题的关键是分类画出图形,也是解本题的难点.

| A. | 0.5×10-8s | B. | 5×10-9s | C. | 5×10-8s | D. | 0.5×10-9s |
| A. | a2+2a3=3a5 | B. | a•a2=a3 | C. | a6÷a2=a3 | D. | (a2)3=a5 |
| A. | 正方形 | B. | 正六边形 | C. | 正八边形 | D. | 正十二边形 |
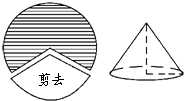 如图,将半径为15cm的圆形纸片剪去$\frac{2}{5}$圆周的一个扇形,用剩下的扇形围成一个圆锥的侧面(接缝忽略不计),这个圆锥的高是( )
如图,将半径为15cm的圆形纸片剪去$\frac{2}{5}$圆周的一个扇形,用剩下的扇形围成一个圆锥的侧面(接缝忽略不计),这个圆锥的高是( )| A. | 12cm | B. | 8cm | C. | 20cm | D. | 18cm |
 如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.求证:AC平分∠DAB.
如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.求证:AC平分∠DAB.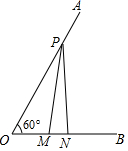 如图,已知∠AOB=60°,点P在边OA上,OP=10,点M、N在边OB上,PM=PN,若MN=2,则OM=( )
如图,已知∠AOB=60°,点P在边OA上,OP=10,点M、N在边OB上,PM=PN,若MN=2,则OM=( )