题目内容
7.用两种正多边形镶嵌,不能与正三角形匹配的正多边形是( )| A. | 正方形 | B. | 正六边形 | C. | 正八边形 | D. | 正十二边形 |
分析 由镶嵌的条件知,在一个顶点处各个内角和为360°.依此即可解答.
解答 解:A、正三角形的每个内角是60°,正方形的每个内角是90°.∵3×60°+2×90°=360°,∴正方形能匹配;
B、正六边形的每个内角是120°,正三角形的每个内角是60度.∵2×120°+2×60°=360°,或120°+4×60°=360°,∴正六边形能匹配;
C、正三角形的每个内角是60°,正八边形内角为135°,显然不能构成360°的周角,故不能匹配.
D、正三角形的每个内角是60°,正十二边形的每个内角是180°-360°÷12=150°,∵60°+2×150°=360°,∴正十二边形能匹配;
故选C.
点评 考查了平面镶嵌(密铺).几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
15.下列图案是轴对称图形但不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
2.某企业今年3月份产值为m万元,4月份比3月份减少了8%,预测5月份比4月份增加9%,则5月份的产值是( )
| A. | (m-8%)(m+9%)万元 | B. | (1-8%)(1+9%)m万元 | C. | (m-8%+9%)万元 | D. | (m-8%+9%)m万元 |
16.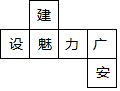 如图是一个正方体的表面展开图,则原正方体中与“魅”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“魅”字所在的面相对的面上标的字是( )
 如图是一个正方体的表面展开图,则原正方体中与“魅”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“魅”字所在的面相对的面上标的字是( )| A. | 建 | B. | 力 | C. | 广 | D. | 安 |
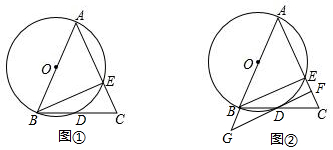
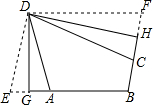 定义:有三个内角相等凸四边形叫三等角四边形.
定义:有三个内角相等凸四边形叫三等角四边形.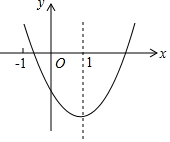 二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论: