题目内容
20.若x-y=4,x+y=7,则x2-y2=28.(-$\frac{3}{5}$)2013$•(\frac{5}{3})$2013=-1.分析 原式利用平方差公式化简,将各自的值代入计算即可求出值;原式逆用积的乘方运算法则变形,计算即可得到结果.
解答 解:∵x-y=4,x+y=7,
∴x2-y2=(x+y)(x-y)=28,
原式=(-$\frac{3}{5}$×$\frac{5}{3}$)2013=(-1)2013=-1.
故答案为:28;-1.
点评 此题考查了平方差公式,以及幂的乘方与积的乘方,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
10.一元二次方程x2-2x-5=0的左边配成完全平方后所得方程为( )
| A. | (x+1)2=6 | B. | (x-1)2=6 | C. | (x+2)2=9 | D. | (x-2)2=9 |
11.有20筐白菜,以每筐25千克为标准,超过或不足的分别用正、负来表示,记录如下:
(1)与标准质量比较,20筐白菜总计超过或不足多少千克?
(2)若白菜每千克售价2.6元,则出售这20筐白菜可卖多少元?
| 与标准质量的差(单位:千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
| 筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(2)若白菜每千克售价2.6元,则出售这20筐白菜可卖多少元?
8.某种电子元件的体积为0.000 000 75毫米3,0.000 000 75用科学记数法表示为( )
| A. | 7.5×10-7 | B. | 0.75×10-7 | C. | 7.5×10-4 | D. | 75×10-6 |
15.下列各式能用平方差公式分解因式的是( )
| A. | x2+y2 | B. | -x2-y2 | C. | -x2+y2 | D. | x2-y3 |
9.3m(a-b)-9n(b-a)的公因式是( )
| A. | 3(a-b) | B. | m+n | C. | 3(a+b) | D. | 3m-9n |
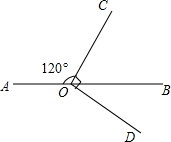 如图,已知∠AOC=120°,∠COD是直角,∠BOC=2∠BOD.问点A、O、B在一条直线上吗?为什么?
如图,已知∠AOC=120°,∠COD是直角,∠BOC=2∠BOD.问点A、O、B在一条直线上吗?为什么?