题目内容
1.大圩村某养殖葡萄户,从葡萄上市到销售完需20天,售价为15元/千克,销售情况在第x天的相关信息如下表所示:| 成本P(元/千克) | 8-$\frac{x}{10}$ |
| 采摘量q(千克) | 1000-10x |
(2)该养殖葡萄户,每天获得的利润为y(元),y关于x的关系是什么?第几天利润最大;
(3)该养殖葡萄户决定,每销售1千克捐养老院m(m≤2)元,满足每天获得的利润随x的增大而增大,求m的取值范围.
分析 (1)根据题意得到第20天每千克的利润最大;
(2)把y=($\frac{x}{10}$+7)q=-x2+30x+7000,配方得到y=-(x-15)2+7225,即可得到结论;
(3)根据题意得到y═($\frac{x}{10}$+7-m)q=-[x-(15+5m)]2+7225+25m2-850m,由于对称轴x=15+5m≥20,解得m≥1,于是得到结论.
解答 解:(1)第20天每千克的利润最大,
∵15-P=$\frac{x}{10}$+7,
∵$\frac{1}{10}$>0,
∴每天没千克利润随着天数的增加而增加;
(2)y=($\frac{x}{10}$+7)q=-x2+30x+7000,
配方得:y=-(x-15)2+7225,
∴第15天的利润最大,最大利润为:7225元;
(3)y═($\frac{x}{10}$+7-m)q=-[x-(15+5m)]2+7225+25m2-850m,
∵对称轴x=15+5m≥20,
∴m≥1,
∴m的取值范围:1≤m≤2.
点评 本题考查了二次函数的应用,理解利润的计算方法,理解利润=每千克的利润×销量是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.有20筐白菜,以每筐25千克为标准,超过或不足的分别用正、负来表示,记录如下:
(1)与标准质量比较,20筐白菜总计超过或不足多少千克?
(2)若白菜每千克售价2.6元,则出售这20筐白菜可卖多少元?
| 与标准质量的差(单位:千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
| 筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(2)若白菜每千克售价2.6元,则出售这20筐白菜可卖多少元?
9.3m(a-b)-9n(b-a)的公因式是( )
| A. | 3(a-b) | B. | m+n | C. | 3(a+b) | D. | 3m-9n |
16.某种服装每件的标价是a元,按标价的七折销售时,仍可获利10%,则这件服装每件的进价为( )
| A. | $\frac{0.7a}{1+10%}$元 | B. | $\frac{0.7a}{1-10%}$元 | C. | 0.7×(1-10%)a元 | D. | 0.7×(1+10%)a元 |
11.聪聪的文件夹里放了大小相同的试卷共12页,其中语文6页,数学4页,英语2页,他随机地从讲义夹中抽出1页,抽出的试卷恰好是数学试卷的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
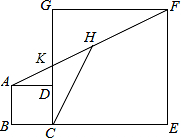 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,连结AF交CG于点K,H是AF的中点,连结CH.
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,连结AF交CG于点K,H是AF的中点,连结CH.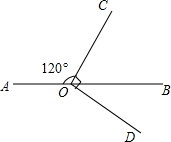 如图,已知∠AOC=120°,∠COD是直角,∠BOC=2∠BOD.问点A、O、B在一条直线上吗?为什么?
如图,已知∠AOC=120°,∠COD是直角,∠BOC=2∠BOD.问点A、O、B在一条直线上吗?为什么?