题目内容
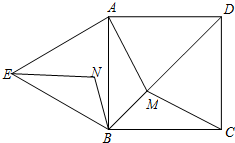 如图,四边形ABCD是边长为
如图,四边形ABCD是边长为| 2 |
(1)求证:△AMB≌△ENB;
(2)①当M点在何处时,AM+CM的值最小;
②当M点在何处时,AM+BM+CM的值最小,并求出这个最小值.
考点:四边形综合题
专题:综合题
分析:(1)根据旋转的性质得BM=BN,∠MBN=60°,则可判断△ABE是等边三角形,得到BA=BE,∠ABE=60°,易得∠ABM=∠EBN,然后根据“SAS”可判断△AMB≌△ENB;
(2)①连接AC,AC与BD相交于点O,如图1,根据正方形的性质得AC=2,点O为BD的中点,根据两点之间线段最短得到AM+CM≥AC(当M点在AC上时取等号),于是得到当M点在BD的中点时,AM+CM的值最小;
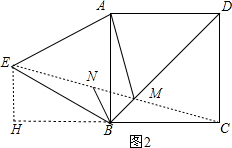
②由△BMN为等边三角形得BM=MN,由△AMB≌△ENB得EN=AM,根据两点之间线段最短,当点E、N、M、C共线时,AM+BM+CM的值最小,如图2,作EH⊥BC于H,先计算出∠EBH=30°,在Rt△EBH中,根据含30度的直角三角形三边的关系得到EH=
BE=
,BH=
EH=
,然后在Rt△EHC中,根据勾股定理可计算出CE=
+1.
(2)①连接AC,AC与BD相交于点O,如图1,根据正方形的性质得AC=2,点O为BD的中点,根据两点之间线段最短得到AM+CM≥AC(当M点在AC上时取等号),于是得到当M点在BD的中点时,AM+CM的值最小;
②由△BMN为等边三角形得BM=MN,由△AMB≌△ENB得EN=AM,根据两点之间线段最短,当点E、N、M、C共线时,AM+BM+CM的值最小,如图2,作EH⊥BC于H,先计算出∠EBH=30°,在Rt△EBH中,根据含30度的直角三角形三边的关系得到EH=
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| ||
| 2 |
| 3 |
解答:(1)证明:∵BM绕点B逆时针旋转60°得到BN,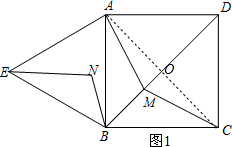
∴BM=BN,∠MBN=60°,
∵△ABE是等边三角形,
∴BA=BE,∠ABE=60°,
∵∠ABM+∠ABN=60°,∠EBN+∠ABN=60°,
∴∠ABM=∠EBN,
在△AMB和△ENB中,
,
∴△AMB≌△ENB(SAS);
(2)解:①连接AC,AC与BD相交于点O,如图1,
∵四边形ABCD是边长为
的正方形,
∴AC=
×
=2,点O为BD的中点,
∵AM+CM≥AC(当M点在AC上时取等号),
∴当M点在BD的中点时,AM+CM的值最小,最小值为2;
②∵△BMN为等边三角形,
∴BM=MN,
∵△AMB≌△ENB,
∴EN=AM,
∴当点E、N、M、C共线时,AM+BM+CM的值最小,如图2,
作EH⊥BC于H,
∵∠ABE=60°,∠ABC=90°,
∴∠EBH=30°,
在Rt△EBH中,EH=
BE=
,
BH=
EH=
,
在Rt△EHC中,CH=BH+BC=
+
,
∴CE2=CH2+EH2=(
+
)2+(
)2=4+2
=(
+1)2,
∴CE=
+1,
∴当M点在CE上时,AM+BM+CM的值最小,这个最小值为
+1.

∴BM=BN,∠MBN=60°,
∵△ABE是等边三角形,
∴BA=BE,∠ABE=60°,
∵∠ABM+∠ABN=60°,∠EBN+∠ABN=60°,
∴∠ABM=∠EBN,
在△AMB和△ENB中,
|

∴△AMB≌△ENB(SAS);
(2)解:①连接AC,AC与BD相交于点O,如图1,
∵四边形ABCD是边长为
| 2 |
∴AC=
| 2 |
| 2 |
∵AM+CM≥AC(当M点在AC上时取等号),
∴当M点在BD的中点时,AM+CM的值最小,最小值为2;
②∵△BMN为等边三角形,
∴BM=MN,
∵△AMB≌△ENB,
∴EN=AM,
∴当点E、N、M、C共线时,AM+BM+CM的值最小,如图2,
作EH⊥BC于H,
∵∠ABE=60°,∠ABC=90°,
∴∠EBH=30°,
在Rt△EBH中,EH=
| 1 |
| 2 |
| ||
| 2 |
BH=
| 3 |
| ||
| 2 |
在Rt△EHC中,CH=BH+BC=
| ||
| 2 |
| 2 |
∴CE2=CH2+EH2=(
| ||
| 2 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
∴CE=
| 3 |
∴当M点在CE上时,AM+BM+CM的值最小,这个最小值为
| 3 |
点评:本题考查了四边形的综合题:熟练掌握正方形性质、等边三角形的判定与性质、全等三角形的判定与性质和旋转的性质;会利用含30度的直角三角形三边的关系和勾股定理进行计算;会运用两点之间线段最短解决有关线段的和的最小值问题.

练习册系列答案
相关题目
下列命题是假命题的是( )
| A、同旁内角互补 |
| B、垂直于同一条直线的两条直线平行 |
| C、对顶角相等 |
| D、同角的余角相等 |
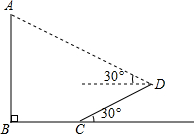 已知,如图,树AB在阳光下的投影是BCD,斜坡CD的坡角为30°,阳光在这时与地面所成的角度为30°,测得BC=3米,CD=2米,求树AB的高.(已知
已知,如图,树AB在阳光下的投影是BCD,斜坡CD的坡角为30°,阳光在这时与地面所成的角度为30°,测得BC=3米,CD=2米,求树AB的高.(已知
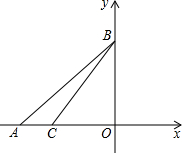 如图,在平面直角坐标系中,点A(-9,0)在x轴的负半轴上,点B在y轴的正半轴上,点C在线段OA上,AC:CO=1:2,△ABC的面积为12,动点P从C出发,沿线段CB以每秒1个单位的速度向终点B运动,同时动点Q从A出发沿线段AO以每秒2个单位的速度向终点O运动,Q点到达终点O,P点继续运动至终点B停止运动,
如图,在平面直角坐标系中,点A(-9,0)在x轴的负半轴上,点B在y轴的正半轴上,点C在线段OA上,AC:CO=1:2,△ABC的面积为12,动点P从C出发,沿线段CB以每秒1个单位的速度向终点B运动,同时动点Q从A出发沿线段AO以每秒2个单位的速度向终点O运动,Q点到达终点O,P点继续运动至终点B停止运动,