题目内容
已知抛物线y=ax2+bx+c经过点A(-1,0),B(3,0),C(0,3)三点,直线l是抛物线的对称轴.
(1)求抛物线的解析式.
(2)设点P是l上一个动点,当|PB-PC|最大时求点P的坐标.
(1)求抛物线的解析式.
(2)设点P是l上一个动点,当|PB-PC|最大时求点P的坐标.
考点:待定系数法求二次函数解析式,二次函数的性质
专题:计算题
分析:(1)根据题意设出抛物线解析式为y=a(x+1)(x-3),将C坐标代入求出a的值即可;
(2)连接BC,与直线l交于点P,由两边之差小于第三边得到此时|PB-PC|最大,设直线BC解析式为y=mx+n,将B与C坐标代入求出m与n的值,确定出P坐标即可.
(2)连接BC,与直线l交于点P,由两边之差小于第三边得到此时|PB-PC|最大,设直线BC解析式为y=mx+n,将B与C坐标代入求出m与n的值,确定出P坐标即可.
解答: 解:(1)设抛物线解析式为y=a(x+1)(x-3),
解:(1)设抛物线解析式为y=a(x+1)(x-3),
将C(0,3)代入得:a=-1,
则抛物线解析式为y=-(x+1)(x-3)=-x2+2x+3;
(2)连接BC,与直线l交于点P,此时|PB-PC|最大,
设直线BC解析式为y=mx+n,
将C(0,3),B(3,0)代入得:
,
解得:m=-1,n=3,
此时直线BC解析式为y=-x+3,
令x=1得到y=2,
则此时P(1,2).
 解:(1)设抛物线解析式为y=a(x+1)(x-3),
解:(1)设抛物线解析式为y=a(x+1)(x-3),将C(0,3)代入得:a=-1,
则抛物线解析式为y=-(x+1)(x-3)=-x2+2x+3;
(2)连接BC,与直线l交于点P,此时|PB-PC|最大,
设直线BC解析式为y=mx+n,
将C(0,3),B(3,0)代入得:
|
解得:m=-1,n=3,
此时直线BC解析式为y=-x+3,
令x=1得到y=2,
则此时P(1,2).
点评:此题考查了待定系数法确定二次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
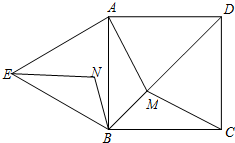 如图,四边形ABCD是边长为
如图,四边形ABCD是边长为 如图,画出△ABC关于BC对称的图形.
如图,画出△ABC关于BC对称的图形.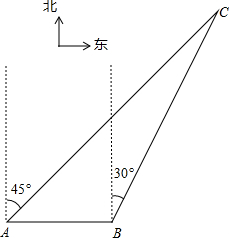 如图,我渔政310船在南海海面上沿正东方向匀速航行,在A地观测到我渔船C在东北方向上的我国某传统渔场,若渔政310船航向不变,航行半小时后到达B处,此时观测到我渔船C在北偏东30°方向上.问渔政310船再航行多久,离我渔船C的距离最近?(假设我渔船C捕鱼时移动距离忽略不计,结果不取近似值)
如图,我渔政310船在南海海面上沿正东方向匀速航行,在A地观测到我渔船C在东北方向上的我国某传统渔场,若渔政310船航向不变,航行半小时后到达B处,此时观测到我渔船C在北偏东30°方向上.问渔政310船再航行多久,离我渔船C的距离最近?(假设我渔船C捕鱼时移动距离忽略不计,结果不取近似值) 如图,在⊙O中,若已知∠BAC=48°,则∠BC0=
如图,在⊙O中,若已知∠BAC=48°,则∠BC0=