题目内容
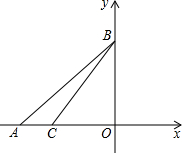 如图,在平面直角坐标系中,点A(-9,0)在x轴的负半轴上,点B在y轴的正半轴上,点C在线段OA上,AC:CO=1:2,△ABC的面积为12,动点P从C出发,沿线段CB以每秒1个单位的速度向终点B运动,同时动点Q从A出发沿线段AO以每秒2个单位的速度向终点O运动,Q点到达终点O,P点继续运动至终点B停止运动,
如图,在平面直角坐标系中,点A(-9,0)在x轴的负半轴上,点B在y轴的正半轴上,点C在线段OA上,AC:CO=1:2,△ABC的面积为12,动点P从C出发,沿线段CB以每秒1个单位的速度向终点B运动,同时动点Q从A出发沿线段AO以每秒2个单位的速度向终点O运动,Q点到达终点O,P点继续运动至终点B停止运动,(1)求直线BC的解析式;
(2)设动点P的运动时间为t秒,△PAQ的面积为S,求S与t之间的函数关系,并直接写出自变量t的取值范围;
(3)在(2)的条件下以Q点为圆心,以t个单位为半径作⊙Q,求t为何值时,点P在⊙Q上.
考点:一次函数综合题
专题:
分析:(1)根据A点坐标和已知条件可得C点坐标,根据三角形面积公式可得B点坐标,再根据待定系数法可得直线BC的解析式;
(2)过P作PH⊥OC于H.根据三角函数得到PH=
t,根据勾股定理得到BC,再分两种情况:0<t≤
;
<t≤10;讨论可求S与t之间的函数关系;
(3)分三种情况:①Q与C重合;②Q在OC上;③Q在O点,P点继续运动;讨论可求点P在⊙Q上时t的值.
(2)过P作PH⊥OC于H.根据三角函数得到PH=
| 4 |
| 5 |
| 9 |
| 2 |
| 9 |
| 2 |
(3)分三种情况:①Q与C重合;②Q在OC上;③Q在O点,P点继续运动;讨论可求点P在⊙Q上时t的值.
解答:解:(1)∵A(-9,0),
∴OA=9,
∵AC:CO=1:2,
∴AC=3,OC=6,
∴C(-6,0),
∵ABC的面积=
AC•DB=12,
∴OB=8,
∴B(0,8),
设直线BC的解析式为y=kx+b,则
,
解得
.
故直线BC的解析式为y=
x+8;
 (2)过P作PH⊥OC于H.
(2)过P作PH⊥OC于H.
PH=CP•sin∠BCO=
t,
在Rt△OBC中,BC=
=10,
则S=
;
(3)∵P在⊙O上,
∴OP=t,
分三种情况:
①Q与C重合,
2t=3,
解得t=
;
②Q在OC上,
∵CP=PQ=t,
∴CH=QH=
t,
t+3=2t,
解得t=
;
③Q在O点,P点继续运动,
t+3=9,
解得t=5.
∴OA=9,
∵AC:CO=1:2,
∴AC=3,OC=6,
∴C(-6,0),
∵ABC的面积=
| 1 |
| 2 |
∴OB=8,
∴B(0,8),
设直线BC的解析式为y=kx+b,则
|
解得
|
故直线BC的解析式为y=
| 4 |
| 3 |
 (2)过P作PH⊥OC于H.
(2)过P作PH⊥OC于H.PH=CP•sin∠BCO=
| 4 |
| 5 |
在Rt△OBC中,BC=
| 62+82 |
则S=
|
(3)∵P在⊙O上,
∴OP=t,
分三种情况:
①Q与C重合,
2t=3,
解得t=
| 3 |
| 2 |
②Q在OC上,
∵CP=PQ=t,
∴CH=QH=
| 3 |
| 5 |
| 6 |
| 5 |
解得t=
| 15 |
| 4 |
③Q在O点,P点继续运动,
| 6 |
| 5 |
解得t=5.
点评:考查了一次函数综合题,涉及的知识点有:三角形面积,待定系数法求直线的解析式,三角函数,勾股定理,分类思想的应用,综合性较强,难度较大.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
 如图,四边形ABCD是边长为
如图,四边形ABCD是边长为 如图,在△ABC中,∠C=90°,sinA=
如图,在△ABC中,∠C=90°,sinA=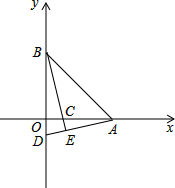 在平面直角坐标系中,已知A,B两点分别在x轴,y轴上,OA=OB=4,C在线段OA上,AC=3,过点A作AE⊥BC,交BC的延长线于E,直线AE交y轴于D.
在平面直角坐标系中,已知A,B两点分别在x轴,y轴上,OA=OB=4,C在线段OA上,AC=3,过点A作AE⊥BC,交BC的延长线于E,直线AE交y轴于D. 如图,画出△ABC关于BC对称的图形.
如图,画出△ABC关于BC对称的图形.