题目内容
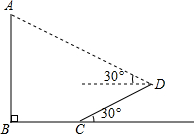已知，如图，树AB在阳光下的投影是BCD，斜坡CD的坡角为30°，阳光在这时与地面所成的角度为30°，测得BC=3米，CD=2米，求树AB的高．（已知| 3 |
考点：解直角三角形的应用-坡度坡角问题
专题：计算题
分析：过D作DE⊥AB，CF⊥DE，可得EF=BC=3米，BE=CF，在直角三角形FCD中，利用30度角所对的直角边等于斜边的一半求出FC的长，利用勾股定理求出DF的长，由EF+FD求出DE的长，在直角三角形ADE中，利用锐角三角函数定义求出AE的长，由AE+EB即可求出AB的长．
解答：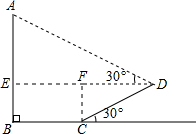
解：过D作DE⊥AB，CF⊥DE，可得EF=BC=3米，BE=CF，
在Rt△FCD中，∠FDC=30°，CD=2米，
∴FC=BE=
CD=1米，DF=
=
米，
∴DE=DF+FE=（
+3）米，
在Rt△ADE中，∠ADE=30°，
∴AE=EDtan30°=（
+3）×
=1+
≈2.24（米），
则树高AB为3.24米．
解：过D作DE⊥AB，CF⊥DE，可得EF=BC=3米，BE=CF，在Rt△FCD中，∠FDC=30°，CD=2米，
∴FC=BE=
| 1 |
| 2 |
| CD2-CF2 |
| 3 |
∴DE=DF+FE=（
| 3 |
在Rt△ADE中，∠ADE=30°，
∴AE=EDtan30°=（
| 3 |
| ||
| 3 |
| 3 |
则树高AB为3.24米．
点评：此题考查了解直角三角形的应用-坡度坡角问题，熟练掌握直角三角形的性质是解本题的关键．
练习册系列答案
相关题目
下列计算结果正确的是（ ）
| A、（2x5）3=6x15 |
| B、（-x4）3=-x12 |
| C、（2x3）2=2x6 |
| D、[（-x）3]4=x7 |
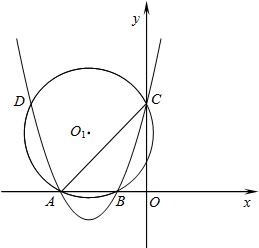抛物线y=ax2+bx+3与x轴相交于点A（-3，0），B（-1，0），与y轴相交于点C，⊙O1为△ABC的外接圆，交抛物线于另一点D．
热气球是用热空气作为浮升气体的气球，人们可以利用它在空中进行飞行．某一天，热气球爱好者小明乘坐热气球在空中A处测得地面一建筑物M的俯角为30°，测得另一建筑物N的俯角为45°（如图），此时热气球离地面的高度为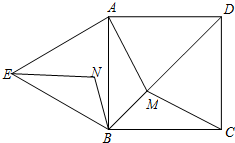
如图，四边形ABCD是边长为
如图，画出△ABC关于BC对称的图形．