题目内容
7.若|a|=1,|b|=2,|c|=3,且a>b>c,则a+b-c=0或2.分析 首先根据绝对值确定a,b,c的可能数值,然后根据a>b>c,即可确定a,b,c的值,从而求解.
解答 解:由|a|=1,|b|=2,|c|=3,知a=±1,b=±2,c=±3,
又因为a>b>c,故b=-2,c=-3,则
①当a=1时,a+b-c=1+(-2)-(-3)=2;
②当a=-1时,a+b-c=-1+(-2)-(-3)=0.
故答案为0或2.
点评 本题主要考查了绝对值的性质,若|x|=a(a>0),则x=a或-a.正确确定a,b,c的值是解决本题的关键.

练习册系列答案
相关题目
15.$\frac{1}{2}$,$\frac{1}{2}$,$\frac{1}{2}$,$\frac{7}{16}$,$\frac{11}{32}$,( )
| A. | $\frac{15}{64}$ | B. | $\frac{1}{4}$ | C. | $\frac{13}{48}$ | D. | $\frac{1}{3}$ |
17.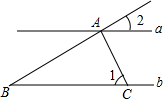 如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠1=55°,则∠2的度数是( )
如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠1=55°,则∠2的度数是( )
 如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠1=55°,则∠2的度数是( )
如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠1=55°,则∠2的度数是( )| A. | 35° | B. | 25° | C. | 65° | D. | 50° |
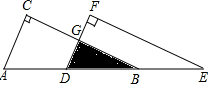 如图将Rt△ABC沿斜边AB向右平移5cm,得到Rt△DEF.已知AB=10cm,BC=8cm.求图中阴影部分三角形的周长.
如图将Rt△ABC沿斜边AB向右平移5cm,得到Rt△DEF.已知AB=10cm,BC=8cm.求图中阴影部分三角形的周长.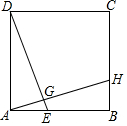 如图,正方形ABCD中,H在BC上,DE⊥AH交AB于点E,交AH于点G,若AB=3,BH=1.
如图,正方形ABCD中,H在BC上,DE⊥AH交AB于点E,交AH于点G,若AB=3,BH=1. 如图,正方形ABCD和CEFG的边长分别为m、n,试用m、n的代数式表示三角形BDF的面积S.
如图,正方形ABCD和CEFG的边长分别为m、n,试用m、n的代数式表示三角形BDF的面积S.