题目内容
4. 已知:△ABC内部一点O到两边AB、AC所在直线的距离相等,且OB=OC.
已知:△ABC内部一点O到两边AB、AC所在直线的距离相等,且OB=OC.求证:AB=AC.
分析 证明Rt△BOF≌Rt△COE,根据全等三角形的性质得到∠FBO=∠ECO,根据等腰三角形的性质得到∠CBO=∠BCO,得到∠ABC=∠ACB,根据等腰三角形的判定定理证明结论.
解答 证明:在Rt△BOF和Rt△COE中,
$\left\{\begin{array}{l}{OF=OE}\\{OB=OC}\end{array}\right.$,
∴Rt△BOF≌Rt△COE,
∴∠FBO=∠ECO,
∵OB=OC,
∴∠CBO=∠BCO,
∴∠ABC=∠ACB,
∴AB=AC.
点评 本题考查的是角平分线的性质、全等三角形的判定,掌握全等三角形的判定定理、等腰三角形的判定定理是解题的关键.

练习册系列答案
相关题目
 如图,在?ABCD中,CE平分∠BCD,交AD于点E,DF平分∠ADC,交BC于点F,CE与DF交于点P,连接EF,BP.
如图,在?ABCD中,CE平分∠BCD,交AD于点E,DF平分∠ADC,交BC于点F,CE与DF交于点P,连接EF,BP.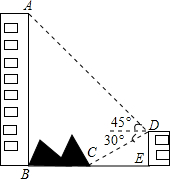 如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=50m,DE=10m,求障碍物B,C两点间的距离(结果精确到1m,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=50m,DE=10m,求障碍物B,C两点间的距离(结果精确到1m,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732) 已知:如图,点G是CA的延长线上一点,CE交AB于点F,AD∥GE,且∠AGF=∠AFG.求证:AD平分∠BAC.
已知:如图,点G是CA的延长线上一点,CE交AB于点F,AD∥GE,且∠AGF=∠AFG.求证:AD平分∠BAC.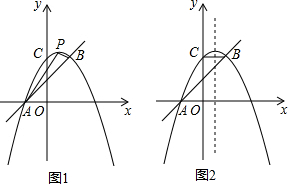
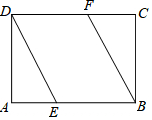 如图,E、F分别是矩形ABCD的边AB、CD上一点,且AE=CF,连接BF、DE.
如图,E、F分别是矩形ABCD的边AB、CD上一点,且AE=CF,连接BF、DE.