Question

13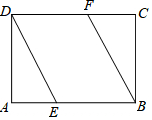．如图，E、F分别是矩形ABCD的边AB、CD上一点，且AE=CF，连接BF、DE．
（1）判断四边形DEBF的形状并说明理由；
（2）若AB=8，AD=4，当四边形DEBF是菱形时，求AE的长．

Answer 1

分析 （1）根据一组对边平行且相等判断四边形DEBF是平行四边形即可；
（2）根据有一组邻边相等的平行四边形是菱形即可求出AE的值．

解答 解：（1）四边形DEBF是平行四边形．
∵四边形ABCD是矩形，
∴CD=AB，DF∥BE，
∵AE=CF，
∴BE=DF，
又∵DF∥BE，
∴四边形DEBF是平行四边形．
（2）设AE=x，
∵四边形DEBF是菱形
∴DE=BE=8-x，
在Rt△DAE中，AD²+AE²=DE²，
即x²+4²=（8-x）²，
解得x=3，
故AE的长为3．

点评 本题考查平行四边形和菱形的判定，难度适中，解题关键是熟练掌握它们的判定方法并灵活运用．