题目内容
8.操作:如图1,直线a、b相较于点O,请你利用尺规作图的方法在图中构造一对以O为公共顶点、且两边分别在直线a、b上的全等三角形.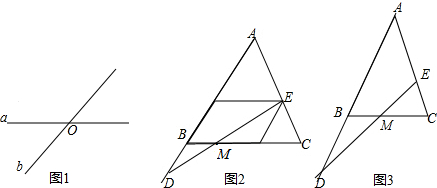
应用:如图2,在等腰△ABC中,AB=AC,点E在线段AC上,点D在边AB的延长线上,若BD=CE,请判断线段MD和线段ME的数量关系,并证明你的结论.
拓展:如图3,在等腰△ABC中,AB=AC,点E在线段AC上,点D在边AB的延长线上,若BD=mCE(m>1),请判断线段MD和线段ME的数量关系,并证明你的结论.
分析 操作:根据边角边定理作图即可;
应用:证明△DBM≌△EFM,根据全等三角形的性质定理得到答案;
拓展:过点E作EF∥AB交CB于点G,证明△DBM∽△EGM,得到答案.
解答 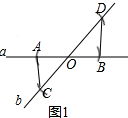 解:在直线a上点O的两侧取OA=OB,
解:在直线a上点O的两侧取OA=OB,
在直线b上点O的两侧取OC=OD,连接AC、BD,
则△AOC≌△BOD;
应用:MD=ME;
证明:∵AB=AC,∴∠ABC=∠C,
又∵EF∥AB,
∴∠EFC=∠C,∴EF=EC,
又∵BD=EC,∴EF=BD,
又∵EF∥AB,∴∠ADM=∠MEF,
在△DBM和△EFM中,
$\left\{\begin{array}{l}{∠BDE=∠FEM}\\{∠BMD=∠FME}\\{BD=EF}\end{array}\right.$,
∴△DBM≌△EFM,
∴DM=EM;
拓展:MD=mME,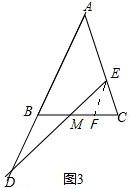
过点E作EF∥AB交CB于点G,
可证△DBM∽△EGM,
∴BD:EG=DM:EM=m
∵AB=AC,∴∠ABC=∠C,
又∵EG∥AB,∴∠ABC=∠EGC,
∴∠EGC=∠C,∴EG=EC,
∴BD:EG=DM:EM=BD:EC=m,
∴MD=mME.
点评 本题考查的是三角形全等的判定和性质,掌握全等三角形的判定定理和性质定理、相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
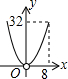
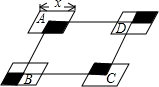 如图,平行四边形ABCD的边长AD为8,面积为32,四个全等的小平行四边形对称中心分别在平行四边形ABCD的顶点上,它们的各边与平行四边形ABCD的各边分别平行,且与平行四边形ABCD相似.若平行四边形的一边长为x,且0<x≤8,阴影部分的面积和为y,则y与x之间的函数关系的大致图象是( )
如图,平行四边形ABCD的边长AD为8,面积为32,四个全等的小平行四边形对称中心分别在平行四边形ABCD的顶点上,它们的各边与平行四边形ABCD的各边分别平行,且与平行四边形ABCD相似.若平行四边形的一边长为x,且0<x≤8,阴影部分的面积和为y,则y与x之间的函数关系的大致图象是( )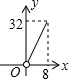
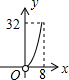
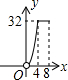
 如图,已知OA=OB.
如图,已知OA=OB. 抛物线y=ax2+bx+c的图象大致如图所示,有下列说法:①a>0,b<0,c<0;②;a-b+c>0;③b2-4ac<0;④直线y=ax+c与此抛物线有两个交点,其中正确的有( )个.
抛物线y=ax2+bx+c的图象大致如图所示,有下列说法:①a>0,b<0,c<0;②;a-b+c>0;③b2-4ac<0;④直线y=ax+c与此抛物线有两个交点,其中正确的有( )个.