题目内容
4.化简求值:$\frac{x+1}{{x}^{2}-1}$+$\frac{x+1}{x-1}$÷(2-x-$\frac{5x-1}{x-1}$),其中x=2cos45°.分析 先根据分式混合运算的法则把原式进行化简,再求出x的值,代入原式进行计算即可.
解答 解:原式=$\frac{1}{x-1}$+$\frac{x+1}{x-1}$÷$\frac{-(x+1)^{2}}{x-1}$
=$\frac{1}{x-1}$+$\frac{x+1}{x-1}$•$\frac{x-1}{-(x+1)^{2}}$
=$\frac{1}{x-1}$+$\frac{1}{-(x+1)}$
=$\frac{1}{x-1}$-$\frac{1}{x+1}$
=$\frac{2}{(x+1)(x-1)}$,
当x=2cos45°=2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$时,原式=$\frac{2}{(\sqrt{2}+1)(\sqrt{2}-1)}$=2.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
15.为了看图钉落地后钉尖着地的概率有多大,小明做了大量重复试验,发现钉尖着地的次数是实验总次数的40%,下列说法错误的是( )
| A. | 钉尖着地的频率是0.4 | |
| B. | 随着试验次数的增加,钉尖着地的频率稳定在0.4附近 | |
| C. | 钉尖着地的概率约为0.4 | |
| D. | 前20次试验结束后,钉尖着地的次数一定是8次 |
12.下列计算中,正确的是( )
| A. | x2+x4=x6 | B. | 2x+3y=5xy | C. | (x3)2=x6 | D. | x6÷x3=x2 |
19.一个形如圆锥冰淇淋纸筒,其底面直径为6cm,母线长为10cm,围成这样的冰淇淋纸筒所需纸的面积是( )
| A. | 60πcm2 | B. | 30πcm2 | C. | 28πcm2 | D. | 15πcm2 |
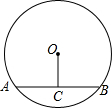 如图,⊙O的半径为5cm,圆心O到AB的距离为3cm,则弦AB长为8 cm.
如图,⊙O的半径为5cm,圆心O到AB的距离为3cm,则弦AB长为8 cm.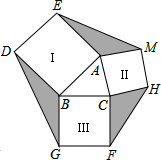 如图,已知△ABC,BC=5,AB=4,分别以AB、BC、CA为边向外作正方形,则图中阴影部分的面积之和的最大值是30.
如图,已知△ABC,BC=5,AB=4,分别以AB、BC、CA为边向外作正方形,则图中阴影部分的面积之和的最大值是30.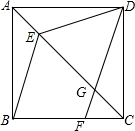 如图,在正方形ABCD中,点E在对角线AC上,点F在边BC上,联结BE、DF,DF交对角线AC于点G,且DE=DG;
如图,在正方形ABCD中,点E在对角线AC上,点F在边BC上,联结BE、DF,DF交对角线AC于点G,且DE=DG;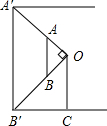 小明在数学课上学习了“相似三角形”这一节内容后,回家想用所学到的知识去测量他家小区路灯的高度,他带上了一个自制的直角三角板与皮尺对他家小区的路灯开始进行测量,通过观察可知路灯灯泡的高度与灯杆高度一致.首先,小明手拿自制直角三角板移动位置并观察,使三角板的顶点A与路灯最高点A′在一条线上,顶点B与路灯底端B′在一条线上,并记录下此时所在位置点C,再用皮尺测量出灯杆底端B′到C的距离为2m,小明知道自己的身高为1.6m(眼睛到头顶的距离可忽略不计),请你根据以上数据计算路灯高度A′B′.
小明在数学课上学习了“相似三角形”这一节内容后,回家想用所学到的知识去测量他家小区路灯的高度,他带上了一个自制的直角三角板与皮尺对他家小区的路灯开始进行测量,通过观察可知路灯灯泡的高度与灯杆高度一致.首先,小明手拿自制直角三角板移动位置并观察,使三角板的顶点A与路灯最高点A′在一条线上,顶点B与路灯底端B′在一条线上,并记录下此时所在位置点C,再用皮尺测量出灯杆底端B′到C的距离为2m,小明知道自己的身高为1.6m(眼睛到头顶的距离可忽略不计),请你根据以上数据计算路灯高度A′B′.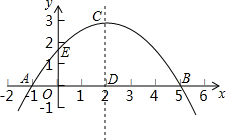 如图,抛物线y=ax2+bx+$\frac{5}{3}$经过点A(-1,0),对称轴方程x=2,请解答下列问题:
如图,抛物线y=ax2+bx+$\frac{5}{3}$经过点A(-1,0),对称轴方程x=2,请解答下列问题: