题目内容
6.在四边形ABCD中,AC、BD交于点O,在下列各组条件中,不能判定四边形ABCD为矩形的是( )| A. | AB=CD,AD=BC,AC=BD | B. | AO=CO,BO=DO,∠A=90° | ||
| C. | ∠A=∠C,∠B+∠C=180°,AC⊥BD | D. | ∠A=∠B=90°,AC=BD |
分析 由AB=CD,AD=BC,得出四边形ABCD是平行四边形,再由对角线相等即可得出A正确;
由AO=CO,BO=DO,得出四边形ABCD是平行四边形,由∠A=90°即可得出B正确;
由∠B+∠C=180°,得出AB∥DC,再证出AD∥BC,得出四边形ABCD是平行四边形,由对角线互相垂直得出四边形ABCD是菱形,C不正确;
由∠A+∠B=180°,得出AD∥BC,由HL证明Rt△ABC≌Rt△BAD,得出BC=AD,证出四边形ABCD是平行四边形,由∠A=90°即可得出D正确.
解答 解:∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
又∵AC=BD,
∴四边形ABCD是矩形,
∴A正确;
∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形,
又∵∠A=90°,
∴四边形ABCD是矩形,
∴B正确;
∵∠B+∠C=180°,
∴AB∥DC,
∵∠A=∠C,
∴∠B+∠A=180°,
∴AD∥BC,
∴四边形ABCD是平行四边形,
又∵AC⊥BD,
∴四边形ABCD是菱形,
∴C不正确;
∵∠A=∠B=90°,
∴∠A+∠B=180°,
∴AD∥BC,如图所示: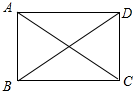
在Rt△ABC和Rt△BAD中,
$\left\{\begin{array}{l}{AC=BD}\\{AB=AB}\end{array}\right.$,
∴Rt△ABC≌Rt△BAD(HL),
∴BC=AD,
∴四边形ABCD是平行四边形,
又∵∠A=90°,
∴四边形ABCD是矩形,
∴D正确;
故选:C.
点评 本题考查了矩形的判定、平行四边形的判定、菱形的判定、全等三角形的判定与性质;熟练掌握矩形的判定方法是解决问题的关键.

练习册系列答案
相关题目
16.若不等式组$\left\{\begin{array}{l}{a-x>0}\\{x+1>0}\end{array}\right.$无解,则a的取值范围是( )
| A. | a≥-1 | B. | a≤-1 | C. | a>-1 | D. | a<-1 |
14.下列多项式相乘,不能用平方差公式的是( )
| A. | (-2y-x)(x+2y) | B. | (x-2y)(-x-2y) | C. | (x-2y)(2y+x) | D. | (2y-x)(-x-2y) |
1.如果方程组$\left\{\begin{array}{l}{x+y=3}\\{5x-y=9}\end{array}\right.$的解是方程3x+my=8的一个解,则m=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
11.下列说法错误的是( )
| A. | 42的算术平方根为4 | B. | $\sqrt{4}$的算术平方根为$\sqrt{2}$ | ||
| C. | $\sqrt{{3}^{2}}$的算术平方根是$\sqrt{3}$ | D. | $\sqrt{81}$的算术平方根是9 |
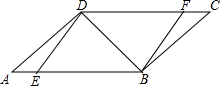 如图,在?ABCD中,点E,F分别在AB,DC上,且ED⊥DB,FB⊥BD.
如图,在?ABCD中,点E,F分别在AB,DC上,且ED⊥DB,FB⊥BD.