题目内容
18.(1)计算:2$\sqrt{3}$-$\sqrt{8}$+$\frac{1}{2}$$\sqrt{12}$+$\frac{1}{5}$$\sqrt{50}$(2)先化简,再求值:(a-$\sqrt{3}$)(a+$\sqrt{3}$)-a(a-6),其中a=$\sqrt{5}$+$\frac{1}{2}$.
分析 (1)首先把每个二次根式进行化简,然后合并同类二次根式即可求解;
(2)首先利用平方差公式计算,合并同类项即可化简,然后代入数值计算即可.
解答 解:(1)原式=2$\sqrt{3}$-2$\sqrt{2}$+$\sqrt{3}$+$\sqrt{2}$=3$\sqrt{3}$-$\sqrt{2}$;
(2)原式=a2-3-a2+6a=6a-3=3(2a-1),
当a=$\sqrt{5}$+$\frac{1}{2}$时,原式=3×2$\sqrt{5}$=6$\sqrt{5}$.
点评 本题考查了二次根式的化简求值,以及平方差公式,正确对式子进行化简是关键.

练习册系列答案
相关题目
6.在四边形ABCD中,AC、BD交于点O,在下列各组条件中,不能判定四边形ABCD为矩形的是( )
| A. | AB=CD,AD=BC,AC=BD | B. | AO=CO,BO=DO,∠A=90° | ||
| C. | ∠A=∠C,∠B+∠C=180°,AC⊥BD | D. | ∠A=∠B=90°,AC=BD |
13.下列二次根式是最简二次根式的是( )
| A. | $\sqrt{a+{b}^{2}}$ | B. | $\sqrt{8x}$ | C. | $\sqrt{{x}^{3}}$ | D. | $\sqrt{\frac{b}{4}}$ |
7.下列命题是假命题的是( )
| A. | 所有的实数都可以用数轴上的点表示 | |
| B. | 过直线外一点有且只有一条直线与已知直线平行 | |
| C. | 两条直线被第三条直线所截,同旁内角互补 | |
| D. | 在同一平面内,垂直于同一条直线的两条直线互相平行 |
8.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{{a^2}+1}$ | C. | $\sqrt{4a}$ | D. | $\sqrt{\frac{1}{3}}$ |
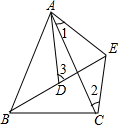 如图,已知AB=AC,AD=AE,BD=CE,且B、D、E三点共线,求证:∠3=∠1+∠2.
如图,已知AB=AC,AD=AE,BD=CE,且B、D、E三点共线,求证:∠3=∠1+∠2. 如图,一次函数y=kx+b与x轴、y轴分别交于A、B两点,则不等式kx+b>1的解集是x<0.
如图,一次函数y=kx+b与x轴、y轴分别交于A、B两点,则不等式kx+b>1的解集是x<0.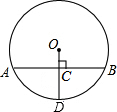 如图,在⊙O中,半径OD垂直于弦AB,垂足为C,OD=13cm,AB=24cm,则CD=8cm.
如图,在⊙O中,半径OD垂直于弦AB,垂足为C,OD=13cm,AB=24cm,则CD=8cm.