题目内容
14. 如图,已知AD是△ABC的角平分线,且AC=AB+BD,∠C=30°,求∠BAC的度数.
如图,已知AD是△ABC的角平分线,且AC=AB+BD,∠C=30°,求∠BAC的度数.
分析 在AC上截取AE=AB,连接DE,易证△ABD≌△AED,可得DE=BD,∠B=∠AED,即可求得DE=EC,即可求得∠AED的值,即可解题.
解答 解:在AC上截取AE=AB,连接DE,
∵AD是△BAC的角平分线,
∴∠BAD=∠DAE,
在△ABD和△AED中,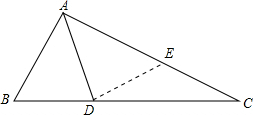
$\left\{\begin{array}{l}{AE=AB}\\{∠BAD=∠DAE}\\{AD=AD}\end{array}\right.$,
∴△ABD≌△AED(SAS),
∴DE=BD,∠B=∠AED,
∵AC=AB+BD,
∴EC=DE,
∴∠EDC=∠C=30°,
∵∠AED=∠EDC+∠C=60°,
∴∠B=∠AED=60°,
∴∠BAC=90°.
点评 本题考查了全等三角形的判定与性质,本题中构造△ABD≌△AED是解题的关键.

练习册系列答案
相关题目
3.在解方程$\frac{x+1}{2}$+$\frac{x-1}{3}$=1时,去分母正确的是( )
| A. | 3x+1-2x-1=1 | B. | 3x+1-2x-1=6 | C. | 3(x+1)+2(x-1)=6 | D. | 3(x+1)-2(x-1)=1 |

 如图是一个全由棱长为1的正方体堆积而成的几何体的俯视图,俯视图上的数字表示此位置的小立方块的个数,求这个几何体的表面积.
如图是一个全由棱长为1的正方体堆积而成的几何体的俯视图,俯视图上的数字表示此位置的小立方块的个数,求这个几何体的表面积.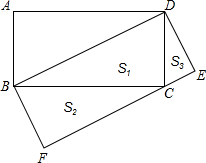 如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.
如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.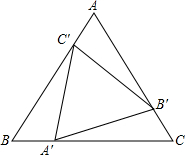 已知:如图所示,点A′,B′,C′分别在等边三角形ABC的三边上,且AC′=BA′=CB′,求证:△A′B′C′是等边三角形.
已知:如图所示,点A′,B′,C′分别在等边三角形ABC的三边上,且AC′=BA′=CB′,求证:△A′B′C′是等边三角形. 如图△ABC,点D,E分别在边AB,AC上,AD•AB=AE•AC,AG平分∠BAC交DE于点F,交BC于点G,若△ADE的面积等于四边形BCED面积的一半,则AF:AG=$\frac{\sqrt{3}}{3}$.
如图△ABC,点D,E分别在边AB,AC上,AD•AB=AE•AC,AG平分∠BAC交DE于点F,交BC于点G,若△ADE的面积等于四边形BCED面积的一半,则AF:AG=$\frac{\sqrt{3}}{3}$.