题目内容
8. 已知:如图,在平面直角坐标系中,O为坐标原点,△OAB的顶点A、B的坐标分别是A(0,5),B(3,1),过点B画BC⊥AB交直线y=-m(m>$\frac{5}{4}$)于点C,连结AC,以点A为圆心,AC为半径画弧交x轴负半轴于点D,连结AD、CD.
已知:如图,在平面直角坐标系中,O为坐标原点,△OAB的顶点A、B的坐标分别是A(0,5),B(3,1),过点B画BC⊥AB交直线y=-m(m>$\frac{5}{4}$)于点C,连结AC,以点A为圆心,AC为半径画弧交x轴负半轴于点D,连结AD、CD.(1)求证:△ABC≌△AOD;
(2)设△ACD的面积为S,求S关于m的函数关系式;
(3)若四边形ABCD恰有一组对边平行,求m的值.
分析 (1)利用两点间的距离公式计算出AB=5,则AB=OA,则可根据“HL”证明△ABC≌△AOD;
(2)过点B作直线BE⊥直线y=-m于E,作AF⊥BE于F,如图,证明Rt△ABF∽Rt△BCE,利用相似比可得BC=$\frac{5}{3}$(m+1),再在Rt△ACB中,由勾股定理得AC2=AB2+BC2=25+$\frac{25}{9}$(m+1)2,然后证明△AOB∽△ACD,利用相似的性质得$\frac{{S}_{△AOB}}{{S}_{△ACD}}$=($\frac{AB}{AC}$)2,而S△AOB=$\frac{15}{2}$,于是可得S=$\frac{5}{6}$(m+1)2+$\frac{15}{2}$(m>$\frac{5}{4}$);
(3)作BH⊥y轴于H,如图,分类讨论:当AB∥CD时,则∠ACD=∠CAB,由△AOB∽△ACD得∠ACD=∠AOB,所以∠CAB=∠AOB,利用三角函数得到tan∠AOB=3,tan∠ACB=$\frac{AB}{BC}$=$\frac{3}{m+1}$,所以$\frac{3}{m+1}$=3;当AD∥BC,则∠5=∠ACB,由△AOB∽△ACD得到∠4=∠5,则∠ACB=∠4,根据三角函数定义得到tan∠4=$\frac{3}{4}$,tan∠ACB=$\frac{AB}{BC}$=$\frac{3}{m+1}$,则$\frac{3}{m+1}$=$\frac{3}{4}$,然后分别解关于m的方程即可得到m的值.
解答 (1)证明:∵A(0,5),B(3,1),
∴AB=$\sqrt{{3}^{2}+(5-1)^{2}}$=5,
∴AB=OA,
∵AB⊥BC,
∴∠ABC=90°,
在Rt△ABC和Rt△AOD中,
$\left\{\begin{array}{l}{AB=AO}\\{AC=AD}\end{array}\right.$,
∴Rt△ABC≌Rt△AOD;
(2)解:过点B作直线BE⊥直线y=-m于E,作AF⊥BE于F,如图,∵∠1+∠2=90°,∠1+∠3=90°,
∴∠2=∠3,
∴Rt△ABF∽Rt△BCE,
∴$\frac{AB}{BC}$=$\frac{AF}{BE}$,即$\frac{5}{BC}$=$\frac{3}{m+1}$,
∴BC=$\frac{5}{3}$(m+1),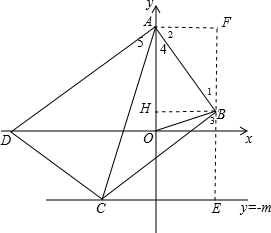
在Rt△ACB中,AC2=AB2+BC2=25+$\frac{25}{9}$(m+1)2,
∵△ABC≌△AOD,
∴∠BAC=∠OAD,即∠4+∠OAC=∠OAC+∠5,
∴∠4=∠5,
而AO=AB,AD=AC,
∴△AOB∽△ACD,
∴$\frac{{S}_{△AOB}}{{S}_{△ACD}}$=($\frac{AB}{AC}$)2=$\frac{25}{25+\frac{25}{9}(m+1)^{2}}$,
而S△AOB=$\frac{1}{2}$×5×3=$\frac{15}{2}$,
∴S=$\frac{5}{6}$(m+1)2+$\frac{15}{2}$(m>$\frac{5}{4}$);
(3)作BH⊥y轴于H,如图,
当AB∥CD时,则∠ACD=∠CAB,
而△AOB∽△ACD,
∴∠ACD=∠AOB,
∴∠CAB=∠AOB,
而tan∠AOB=$\frac{BH}{OH}$=3,tan∠ACB=$\frac{AB}{BC}$=$\frac{5}{\frac{5}{3}(m+1)}$=$\frac{3}{m+1}$
∴$\frac{3}{m+1}$=3,解得m=8;
当AD∥BC,则∠5=∠ACB,
而△AOB∽△ACD,
∴∠4=∠5,
∴∠ACB=∠4,
而tan∠4=$\frac{BH}{AH}$=$\frac{3}{4}$,tan∠ACB=$\frac{AB}{BC}$=$\frac{3}{m+1}$
∴$\frac{3}{m+1}$=$\frac{3}{4}$,
解得m=3.
综上所述,m的值为3或8.
点评 本题考查了相似形的综合题:熟练掌握相似三角形的判定与性质、等腰三角形的性质;合理添加辅助线构造相似图形,然后利用相似的性质计算相应线段的长;同时会利用勾股定理和三角函数的定义进行几何计算;学会运用分类讨论的思想解决数学问题.

| 单科 | 两科 | 三科 | |||||
| 科目 | 数学 | 英语 | 语文 | 语文 数学 | 英语 数学 | 英语 语文 | 语文、数学、英语 |
| 人数 | 32 | 31 | 29 | 16 | 17 | 18 | 10 |
 如图是一个可以自由转动的转盘,如果转动一次转盘,转盘中阴影部分的扇形的圆心角度数为120°.则停止后指针指向阴影部分的概率是$\frac{1}{3}$.
如图是一个可以自由转动的转盘,如果转动一次转盘,转盘中阴影部分的扇形的圆心角度数为120°.则停止后指针指向阴影部分的概率是$\frac{1}{3}$. 如图,抛物线与x轴交于A、B两点,与y轴交于C点,点A的坐标(2,0),点C的坐标为(0,3)它的对称轴是直线x=-1.
如图,抛物线与x轴交于A、B两点,与y轴交于C点,点A的坐标(2,0),点C的坐标为(0,3)它的对称轴是直线x=-1. 如图,A,B是反比例函数y=$\frac{6}{x}$(x>0)图象上的两点,AC⊥x轴于点C,BD⊥x轴于点D,求证:S△AOB=S梯形ABDC.
如图,A,B是反比例函数y=$\frac{6}{x}$(x>0)图象上的两点,AC⊥x轴于点C,BD⊥x轴于点D,求证:S△AOB=S梯形ABDC.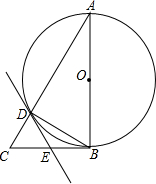 如图所示,△ABC中,∠ABC=90°,点O是AB的中点,以AB为直径作圆与AC交于点D,作∠BDE=∠A,DE与BC交于点E.
如图所示,△ABC中,∠ABC=90°,点O是AB的中点,以AB为直径作圆与AC交于点D,作∠BDE=∠A,DE与BC交于点E.