题目内容
2.如果x1,x2是一元二次方程x2+3x+2=0的两个实数根,那么x1+x2的值是-3.分析 直接根据一元二次方程根与系数的关系得到x1+x2的值.
解答 解:∵x1,x2是一元二次方程x2+3x+2=0的两个实数根,
∴x1+x2=-3,
故答案为:-3.
点评 本题考查了一元二次方程根与系数的关系,方程ax2+bx+c=0的两根为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$,此题难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列各数属于无理数的是( )
| A. | 5 | B. | $\sqrt{4}$ | C. | $\frac{7}{3}$ | D. | $\frac{π}{2}$ |
11.一个布袋中有4个红球与6个白球,除颜色外完全相同,那么从布袋中随机摸一个球是白球的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
12.某校数学课题学习小组在“测量教学楼高度”的活动中,设计了以下两种方案:
请你选择其中的一种方案,求甲教学楼AB和乙教学楼CD的高度.(结果精确到0.1m)
| 课题 | 测量教学楼高度 | |
| 方案 | 方案一 | 方案二 |
| 测量示意图 | 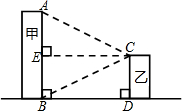 |  |
| 测得数据 | BD=32m,∠ACE=∠BCE=31° | BD=32m,∠DAF=50°,∠CAF=31° |
| 参考数据 | tan31°≈0.60,sin31°≈0.52 cos31°≈0.86 | tan31°≈0.60,tan50°≈1.20, sin50°≈0.77 |
 如图,有两条国道相交于点O,在∠AOB的内部有两村庄C、D,现要修建一加油站P,使点P到OA、OB的距离相等,且使PC=PD,用尺规作图,作出加油站P的位置(不写作法,保留作图痕迹).
如图,有两条国道相交于点O,在∠AOB的内部有两村庄C、D,现要修建一加油站P,使点P到OA、OB的距离相等,且使PC=PD,用尺规作图,作出加油站P的位置(不写作法,保留作图痕迹). 如图,A,B是反比例函数y=$\frac{6}{x}$(x>0)图象上的两点,AC⊥x轴于点C,BD⊥x轴于点D,求证:S△AOB=S梯形ABDC.
如图,A,B是反比例函数y=$\frac{6}{x}$(x>0)图象上的两点,AC⊥x轴于点C,BD⊥x轴于点D,求证:S△AOB=S梯形ABDC.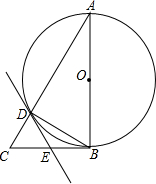 如图所示,△ABC中,∠ABC=90°,点O是AB的中点,以AB为直径作圆与AC交于点D,作∠BDE=∠A,DE与BC交于点E.
如图所示,△ABC中,∠ABC=90°,点O是AB的中点,以AB为直径作圆与AC交于点D,作∠BDE=∠A,DE与BC交于点E.