题目内容
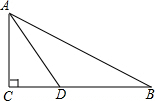如图：在△ABC中，∠C=90°，AD平分∠BAC，AD=BD，CD=2，求AD的长．考点：角平分线的性质,勾股定理
专题：
分析：如图，证明∠B=∠DAB（设为α），证明∠CAD=∠BAD=α；求出α=30°，即可解决问题．
解答：解：如图，∵AD=BD，
∴∠B=∠DAB（设为α），而AD平分∠BAC，
∴∠CAD=∠BAD=α；
∵∠C=90°，
∴∠CAB+∠B=90°，即3α=90°，
∴α=30°，而∠C=90°，
∴AD=2CD=4．
解：如图，∵AD=BD，∴∠B=∠DAB（设为α），而AD平分∠BAC，
∴∠CAD=∠BAD=α；
∵∠C=90°，
∴∠CAB+∠B=90°，即3α=90°，
∴α=30°，而∠C=90°，
∴AD=2CD=4．
点评：该题主要考查了角平分线的性质、直角三角形的性质等几何知识点的应用问题；解题的关键是灵活运用、科学解析、正确解答．
练习册系列答案
提分百分百检测卷系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案
相关题目
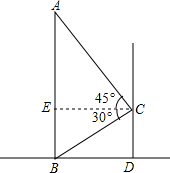如图所示，某中学的教学楼前有一棵大树AB，小明在教学楼的C处测得树顶A的仰角为45°，底部B的俯角为30°，已知大树与教学楼之间的水平距离BD=6m，求AB（结果保留根号）．
如图，在Rt△ABC中，∠ACB=90°，AD平分∠CAB，CE⊥AB交AD于G，DF⊥AB于F，求证：四边形CGFD是菱形．
如图，A、B、C、D是圆上的点，∠1=70°，∠A=40°，求∠D．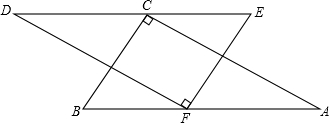
将两块大小相同的直角三角尺（△ABC和△DEF，其中∠A=∠D=30°）按如图所示的位置摆放（直角顶点F在斜边AB上，直角顶点C在斜边DE上），且DE∥AB．
如图，△ABF≌△CDE，∠B=30°，∠DCF=20°，求∠EFC的度数．