题目内容
 如图,△ABF≌△CDE,∠B=30°,∠DCF=20°,求∠EFC的度数.
如图,△ABF≌△CDE,∠B=30°,∠DCF=20°,求∠EFC的度数.考点:全等三角形的性质
专题:
分析:由已知全等三角形的对应角相等推知∠B=∠D=30°;然后由三角形外角定理来求∠EFC的度数.
解答: 解:如图,∵△ABF≌△CDE,∠B=30°,
解:如图,∵△ABF≌△CDE,∠B=30°,
∴∠B=∠D=30°.
又∵∠DCF=20°,
∴∠EFC=∠D+∠DCF=50°.
即∠EFC的度数是50°.
 解:如图,∵△ABF≌△CDE,∠B=30°,
解:如图,∵△ABF≌△CDE,∠B=30°,∴∠B=∠D=30°.
又∵∠DCF=20°,
∴∠EFC=∠D+∠DCF=50°.
即∠EFC的度数是50°.
点评:本题考查了全等三角形的性质.
性质1:全等三角形的对应边相等.
性质2:全等三角形的对应角相等.
性质1:全等三角形的对应边相等.
性质2:全等三角形的对应角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设3x•93-2x=1,则x的值为( )
| A、2 | ||
| B、0 | ||
C、
| ||
| D、3 |
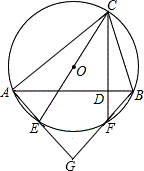 已知△ABC内接于⊙O,CE是⊙O的直径,CD⊥AB于D,CD延长线交⊙O于F,AE,BF的延长线相交于点G.求证:
已知△ABC内接于⊙O,CE是⊙O的直径,CD⊥AB于D,CD延长线交⊙O于F,AE,BF的延长线相交于点G.求证: 如图,在菱形OABC中,∠C=120°,OA=3,对角线OB为半径,以O为圆心画弧,交OA延长线于D,则图中阴影部分的面积为
如图,在菱形OABC中,∠C=120°,OA=3,对角线OB为半径,以O为圆心画弧,交OA延长线于D,则图中阴影部分的面积为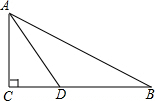 如图:在△ABC中,∠C=90°,AD平分∠BAC,AD=BD,CD=2,求AD的长.
如图:在△ABC中,∠C=90°,AD平分∠BAC,AD=BD,CD=2,求AD的长.
 如图,求∠A+∠B+∠C+∠D+∠E+∠F度数.
如图,求∠A+∠B+∠C+∠D+∠E+∠F度数.