题目内容
7.如图是某校未制作完整的三个年级假期义工(不计报酬,为他人提供服务的人)的统计图,请你根据图中所给信息解答下列问题:(1)请你求出三年级有假期义工12名;
(2)将两幅统计图补充完整;
(3)要求从一年级、三年级义工中各推荐一名队长候选人,二年级义工中推荐两名队长候选人,再从四名候选人中先后选出两人任队长,用列表法或树形图,求出两名队长都是二年级义工的概率是多少?
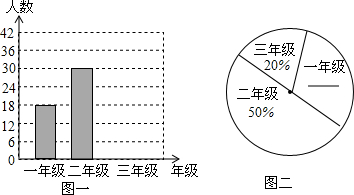
分析 (1)先利用二年级志愿者的人数和它所占的百分比计算出志愿者的总人数为60人,再用60乘以20%得到三年级志愿者的人数,
(2)用100%分别减去二、三年级所占的百分比即可得到一年级志愿者的人数所占的百分比,再把两幅统计图补充完整;
(2)用A表示一年级队长候选人,B、C表示二年级队长候选人,D表示三年级队长候选人,利用树状图展示所有12种等可能的结果,再找出两人都是二年级义工的结果数,然后利用概率公式计算.
解答 解:(1)∵三个年级共有假期义工:30÷50%=60(名);
∴三年级有假期义工为:60×20%=12(名),
故答案为:12;
(2)一年级占的百分比为:100%-20%-50%=30%,
如图所示: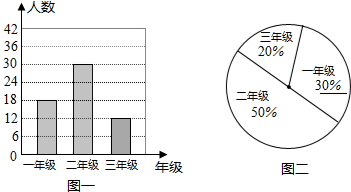
(2)用A表示一年级队长候选人,B、C表示二年级队长候选人,D表示三年级队长候选人,
画树状图得: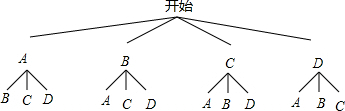 ,
,
∵有12种等可能的结果,其中两人都是八年级义工的情况有两种,
两名队长都是二年级义工的概率为:$\frac{2}{12}$=$\frac{1}{6}$.
点评 此题主要考查了条形统计图以及扇形统计图的应用和树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.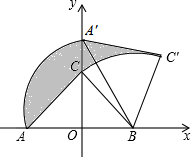 如图,Rt△ABC中,∠ACB=90°,AC=BC=2,在以AB的中点O为坐标原点、AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴正半轴上的A′处,则图中阴影部分面积为( )
如图,Rt△ABC中,∠ACB=90°,AC=BC=2,在以AB的中点O为坐标原点、AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴正半轴上的A′处,则图中阴影部分面积为( )
 如图,Rt△ABC中,∠ACB=90°,AC=BC=2,在以AB的中点O为坐标原点、AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴正半轴上的A′处,则图中阴影部分面积为( )
如图,Rt△ABC中,∠ACB=90°,AC=BC=2,在以AB的中点O为坐标原点、AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴正半轴上的A′处,则图中阴影部分面积为( )| A. | $\frac{4π}{3}$-2 | B. | $\frac{4π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{2π}{3}$-2 |
12.已知在等腰△ABC中,顶角∠A=36°,BD平分∠ABC交AC于点D,则下列说法中错误的是( )
| A. | △ABC∽△BDC | B. | 点D是线段AC的黄金分割点 | ||
| C. | $\frac{AD}{AC}$=$\frac{\sqrt{5}-1}{2}$ | D. | $\frac{AD}{AC}$=$\frac{1}{2}$ |
19.2015年1月份,无锡市某周的日最低气温统计如下表,则这七天中日最低气温的众数和中位数分别是( )
| 日期 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 最低气温/℃ | 2 | 4 | 5 | 3 | 4 | 6 | 7 |
| A. | 4,4 | B. | 5,4 | C. | 4,3 | D. | 4,4.5 |
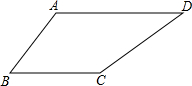 如图,四边形ABCD中,AB=BC=6cm,∠A=120°,∠B=60°,∠C=150°,求AD的长.
如图,四边形ABCD中,AB=BC=6cm,∠A=120°,∠B=60°,∠C=150°,求AD的长.
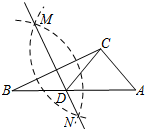 如图,在已知的△ABC中,按以下步骤作图:
如图,在已知的△ABC中,按以下步骤作图: