题目内容
11. 如图,边长为2的正方形ABCD的顶点A在y轴上,顶点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上,已知点B的坐标是($\frac{6}{5}$,$\frac{11}{5}$),则k的值为8.
如图,边长为2的正方形ABCD的顶点A在y轴上,顶点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上,已知点B的坐标是($\frac{6}{5}$,$\frac{11}{5}$),则k的值为8.
分析 过点B作BE⊥y轴于E,过点D作DF⊥y轴于F,根据正方形的性质可得AB=AD,∠BAD=90°,再根据同角的余角相等求出∠BAE=∠ADF,然后利用“角角边”证明△ABE和△DAF全等,根据全等三角形对应边相等可得AF=BE,DF=AE,再求出OF,然后写出点D的坐标,再把点D的坐标代入反比例函数解析式计算即可求出k的值.
解答 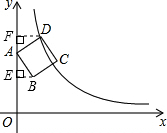 解:如图,过点B作BE⊥y轴于E,过点D作DF⊥y轴于F,
解:如图,过点B作BE⊥y轴于E,过点D作DF⊥y轴于F,
在正方形ABCD中,AB=AD,∠BAD=90°,
∴∠BAE+∠DAF=90°,
∵∠DAF+∠ADF=90°,
∴∠BAE=∠ADF,
在△ABE和△DAF中,
∵$\left\{\begin{array}{l}∠BAE=∠ADF\\∠AEB=∠DFA\\ AB=AD\end{array}\right.$,
∴△ABE≌△DAF(AAS),
∴AF=BE,DF=AE,
∵正方形的边长为2,B($\frac{6}{5}$,$\frac{11}{5}$),
∴BE=$\frac{6}{5}$,AE=$\sqrt{{2}^{2}-(\frac{6}{5})^{2}}$=$\frac{8}{5}$,
∴OF=OE+AE+AF=$\frac{11}{5}$+$\frac{8}{5}$+$\frac{6}{5}$=5,
∴点D的坐标为($\frac{8}{5}$,5),
∵顶点D在反比例函数y=$\frac{k}{x}$(x>0)的图象上,
∴k=xy=$\frac{8}{5}$×5=8.
故答案为:8.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
19.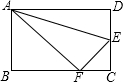 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则tan∠EAF的值是( )
如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则tan∠EAF的值是( )
 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则tan∠EAF的值是( )
如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,则tan∠EAF的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | 2 | D. | 5 |
6.tan30°的结果等于( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{1}{2}$ |
3.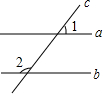 如图,平行线a,b被直线c所截,∠1=42°38′,则∠2的度数为( )
如图,平行线a,b被直线c所截,∠1=42°38′,则∠2的度数为( )
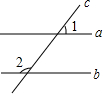 如图,平行线a,b被直线c所截,∠1=42°38′,则∠2的度数为( )
如图,平行线a,b被直线c所截,∠1=42°38′,则∠2的度数为( )| A. | 157°62′ | B. | 137°22′ | C. | 137°62′ | D. | 47°22′ |
20.下列各式正确的是( )
| A. | 20=0 | B. | |-$\sqrt{2}$|=$\sqrt{2}$ | C. | $\sqrt{4}$=±2 | D. | -22=4 |
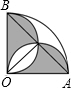 如图,半径为1cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为$\frac{1}{2}$cm2.
如图,半径为1cm,圆心角为90°的扇形OAB中,分别以OA、OB为直径作半圆,则图中阴影部分的面积为$\frac{1}{2}$cm2.