题目内容
9.计算:(1)$\sqrt{2}×3\sqrt{2}$;
(2)2$\sqrt{12}+3\sqrt{1\frac{1}{3}}-\sqrt{5\frac{1}{3}}-\frac{2}{3}\sqrt{48}$;
(3)$\sqrt{48}-\sqrt{54}÷2+(3-\sqrt{3})(1+\frac{1}{\sqrt{3}})$;
(4)(1+$\sqrt{2}$)2(1+$\sqrt{3}$)2(1-$\sqrt{2}$)2(1-$\sqrt{3}$)2.
分析 (1)根据二次根式的乘法法则运算;
(2)先把各二次根式化为最简二次根式,然后合并即可;
(3)利用平方差公式计算;
(4)先变形得到原式=[(1+$\sqrt{2}$)(1-$\sqrt{2}$)]2•[(1+$\sqrt{3}$)(1-$\sqrt{3}$)]2,然后利用平方差公式计算.
解答 解:(1)原式=3×2
=6;
(2)原式=4$\sqrt{3}$+2$\sqrt{3}$-$\frac{4\sqrt{3}}{3}$-$\frac{8\sqrt{3}}{3}$
=2$\sqrt{3}$;
(3)原式=4$\sqrt{3}$-$\frac{3\sqrt{6}}{2}$+$\sqrt{3}$($\sqrt{3}$-1)•$\frac{1}{\sqrt{3}}$($\sqrt{3}$+1)
=4$\sqrt{3}$-$\frac{3\sqrt{6}}{2}$+2;
(4)原式=[(1+$\sqrt{2}$)(1-$\sqrt{2}$)]2•[(1+$\sqrt{3}$)(1-$\sqrt{3}$)]2
=(1-2)2•(1-3)2
=4.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
 如图,∠1的同位角是∠EFG,∠1的内错角是∠BCD;
如图,∠1的同位角是∠EFG,∠1的内错角是∠BCD;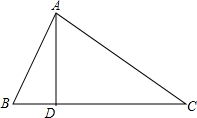 如图,三角形ABC中,AB=10,AC=17,AD与BC交于点D,AD=8,BD=6,求BC的长.
如图,三角形ABC中,AB=10,AC=17,AD与BC交于点D,AD=8,BD=6,求BC的长. (1)请在图中的网格中画三边长分别为:$\sqrt{5}$,$\sqrt{10}$,$\sqrt{13}$的格点△ABC(即顶点都在格点上);
(1)请在图中的网格中画三边长分别为:$\sqrt{5}$,$\sqrt{10}$,$\sqrt{13}$的格点△ABC(即顶点都在格点上);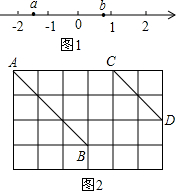 (1)2$\sqrt{12}$-6$\sqrt{\frac{1}{3}}$+3$\sqrt{48}$;
(1)2$\sqrt{12}$-6$\sqrt{\frac{1}{3}}$+3$\sqrt{48}$;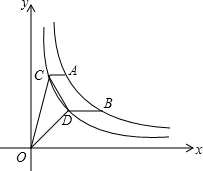 如图,点A、B在双曲线y1=$\frac{k}{x}$(k>1,x>0)上,点C、点D在双曲线y2=$\frac{1}{x}$(x>0)上,AC∥BD∥x轴,若$\frac{AC}{BD}$=m,则△OCD的面积为$\frac{1-{m}^{2}}{2m}$.(用含m的式子表示)
如图,点A、B在双曲线y1=$\frac{k}{x}$(k>1,x>0)上,点C、点D在双曲线y2=$\frac{1}{x}$(x>0)上,AC∥BD∥x轴,若$\frac{AC}{BD}$=m,则△OCD的面积为$\frac{1-{m}^{2}}{2m}$.(用含m的式子表示)