题目内容
1.等边三角形ABC绕其三条中线的交点O旋转,至少要旋转120度才能与原图形重合.分析 根据旋转对称图形的概念:把一个图形绕着一个定点旋转一个角度后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度叫做旋转角.
解答 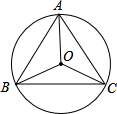 解:∵等边△ABC的中心角为360÷3=120°,
解:∵等边△ABC的中心角为360÷3=120°,
∴旋转120°后即可与原图形重合.
故答案为:120.
点评 此题主要考查了旋转对称图形,本题用到的知识点为:把正多边形旋转它的一个中心角度数之后,可与原来的图形重合.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
12.已知菱形ABCD,点E、F分别在BC、CD上,且△AEF恰为等边三角形,其边长与菱形边长相等,则∠AEB的大小是( )
| A. | 60° | B. | 95° | C. | 80° | D. | 75° |
6.组数为三角形的三边.其中,能构成直角三角形的是( )
| A. | $\sqrt{3}$、$\sqrt{4}$、$\sqrt{5}$ | B. | 32、42、52 | C. | $\frac{1}{3}$、$\frac{1}{4}$、$\frac{1}{5}$ | D. | 3k、4k、5k(k≠0) |
13.若二次函数y=ax2+bx+c的x与y的部分对应值如表,则当x=-1时,y的值为-3.
| x | -7 | -6 | -5 | -4 | -3 | -2 |
| y | -27 | -13 | -3 | 3 | 5 | 3 |
11.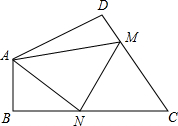 如图,在四边形ABCD中,∠DAB=130°,∠D=∠B=90°,点M,N分别是CD,BC上两个动点,当△AMN的周长最小时,∠AMN+∠ANM的度数为( )
如图,在四边形ABCD中,∠DAB=130°,∠D=∠B=90°,点M,N分别是CD,BC上两个动点,当△AMN的周长最小时,∠AMN+∠ANM的度数为( )
 如图,在四边形ABCD中,∠DAB=130°,∠D=∠B=90°,点M,N分别是CD,BC上两个动点,当△AMN的周长最小时,∠AMN+∠ANM的度数为( )
如图,在四边形ABCD中,∠DAB=130°,∠D=∠B=90°,点M,N分别是CD,BC上两个动点,当△AMN的周长最小时,∠AMN+∠ANM的度数为( )| A. | 90° | B. | 100° | C. | 130° | D. | 140° |
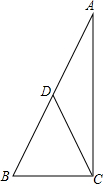 如图,在△ABC中,BC=5cm,AC=12cm,AB=13cm,D为AB的中点,求CD的长.
如图,在△ABC中,BC=5cm,AC=12cm,AB=13cm,D为AB的中点,求CD的长.