题目内容
17．一枚均匀的骰子，六个面分别标有1，2，3，4，5，6，连续抛掷两次朝上的两个数为m，n．（1）求m+n=7的概率；
（2）把（m，n）作为A的坐标，求点在双曲线y=$\frac{6}{x}$上的概率．
分析 （1）列表得出所有等可能的情况数，找出m+n=7的情况数，即可求出所求的概率；
（2）找出mn=6的情况数，即可求出所求的概率．
解答 解：（1）列表如下：
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | （1，1） | （2，1） | （3，1） | （4，1） | （5，1） | （6，1） |
| 2 | （1，2） | （2，2） | （3，2） | （4，2） | （5，2） | （6，2） |
| 3 | （1，3） | （2，3） | （3，3） | （4，3） | （5，3） | （6，3） |
| 4 | （1，4） | （2，4） | （3，4） | （4，4） | （5，4） | （6，4） |
| 5 | （1，5） | （2，5） | （3，5） | （4，5） | （5，5） | （6，5） |
| 6 | （1，6） | （2，6） | （3，6） | （4，6） | （5，6） | （6，6） |
则P=$\frac{6}{36}$=$\frac{1}{6}$；
（2）其中mn=6的情况有4种，
则点在双曲线y=$\frac{6}{x}$上的概率为$\frac{4}{36}$=$\frac{1}{9}$．
点评 此题考查了列表法与树状图法，用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
12．已知菱形ABCD，点E、F分别在BC、CD上，且△AEF恰为等边三角形，其边长与菱形边长相等，则∠AEB的大小是（ ）
| A． | 60° | B． | 95° | C． | 80° | D． | 75° |
6．组数为三角形的三边．其中，能构成直角三角形的是（ ）
| A． | $\sqrt{3}$、$\sqrt{4}$、$\sqrt{5}$ | B． | 32、42、52 | C． | $\frac{1}{3}$、$\frac{1}{4}$、$\frac{1}{5}$ | D． | 3k、4k、5k（k≠0） |
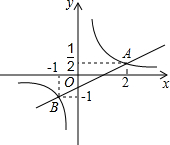如图，在平面直角坐标系中，一次函数y=kx+b（k≠0）的图象与反比例函数y=$\frac{m}{x}$（m≠0）的图象相交于A（2，$\frac{1}{2}$），B（-1，1）两点．