题目内容
20. 如图,∠1的同位角是∠EFG,∠1的内错角是∠BCD;
如图,∠1的同位角是∠EFG,∠1的内错角是∠BCD;①若∠1=∠BCD,则DE∥BC,
根据是内错角相等,两直线平行;
②若FG∥DC,则∠1=∠EFG,
根据是两直线平行,同位角相等.
分析 由图可知∠1和∠EFG是FG、DC被DE所截得到的一对同位角,∠1和∠BCD是DE、BC被CD所截得到的一对内错角,再结合平行线的判定和性质,可得出答案.
解答 解:
∵∠1和∠EFG是FG、DC被DE所截得到的一对同位角,∠1和∠BCD是DE、BC被CD所截得到的一对内错角,
∴∠1的同位角是∠EFG,∠1的内错角是∠BCD;
①若∠1=∠BCD,则 DE∥BC,
根据是 内错角相等,两直线平行;
②若FG∥DC,则∠1=∠EFG,
根据是 两直线平行,同位角相等.
故答案为:∠EFG;∠BCD;DE;BC;内错角相等,两直线平行;∠EFG;两直线平行,同位角相等.
点评 本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.

练习册系列答案
相关题目
15.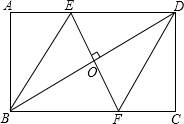 如图,在矩形ABCD中,边AB的长为3,点E、F,分别在AD,BC上,连接BE,DF,EF,BD,若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( )
如图,在矩形ABCD中,边AB的长为3,点E、F,分别在AD,BC上,连接BE,DF,EF,BD,若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( )
 如图,在矩形ABCD中,边AB的长为3,点E、F,分别在AD,BC上,连接BE,DF,EF,BD,若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( )
如图,在矩形ABCD中,边AB的长为3,点E、F,分别在AD,BC上,连接BE,DF,EF,BD,若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( )| A. | 2$\sqrt{3}$ | B. | $\frac{9}{2}$$\sqrt{3}$ | C. | 6$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
12.已知菱形ABCD,点E、F分别在BC、CD上,且△AEF恰为等边三角形,其边长与菱形边长相等,则∠AEB的大小是( )
| A. | 60° | B. | 95° | C. | 80° | D. | 75° |
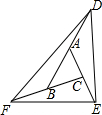 如图,在△ABC中,延长BA使BA=AD,延长AC,使AC=CE,延长CB使CB=BF,则下列结论:①若S△ABC=1,则S△DFB=2; ②S△DFB=S△CEF=S△AED;③△ABC∽△DEF,其中,正确的个数为( )
如图,在△ABC中,延长BA使BA=AD,延长AC,使AC=CE,延长CB使CB=BF,则下列结论:①若S△ABC=1,则S△DFB=2; ②S△DFB=S△CEF=S△AED;③△ABC∽△DEF,其中,正确的个数为( )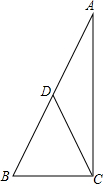 如图,在△ABC中,BC=5cm,AC=12cm,AB=13cm,D为AB的中点,求CD的长.
如图,在△ABC中,BC=5cm,AC=12cm,AB=13cm,D为AB的中点,求CD的长.