题目内容
16.平面直角坐标系中,A(-3,1),B(-1,4),直线AB交x轴于C点,则C点坐标为(-$\frac{11}{3}$,0).分析 利用待定系数法求出直线AB的解析式,令y=0求出x的值即可得出C点的坐标.
解答 解:设直线AB的解析式为y=kx+b(k≠0),
∵A(-3,1),B(-1,4),
∴$\left\{\begin{array}{l}{1=-3k+b}\\{4=-k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{3}{2}}\\{b=\frac{11}{2}}\end{array}\right.$.
∴直线AB的解析式为y=$\frac{3}{2}$x+$\frac{11}{2}$,
∴令y=0,则x=-$\frac{11}{3}$,
∴C(-$\frac{11}{3}$,0).
故答案为:(-$\frac{11}{3}$,0).
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
7.在Rt△ABC中,AB=3,AC=4,则BC的长为( )
| A. | 5 | B. | $\sqrt{7}$ | C. | 5或$\sqrt{7}$ | D. | 无法确定 |
1.下列二次根式为最简二次根式的是( )
| A. | $\sqrt{0.3}$ | B. | $\sqrt{3}$ | C. | $\sqrt{\frac{1}{3}}$ | D. | $\sqrt{44}$ |
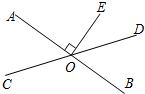 如图,直线AB,CD相交于点O,EO⊥AB,垂足为O.若∠EOD=35°,则∠AOC的度数为55°°.
如图,直线AB,CD相交于点O,EO⊥AB,垂足为O.若∠EOD=35°,则∠AOC的度数为55°°.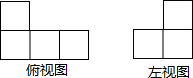 如图,这是由若干个相同的小立方体搭成的几何体俯视图和左视图,则小立方体的个数可能是5个或6个或7个.
如图,这是由若干个相同的小立方体搭成的几何体俯视图和左视图,则小立方体的个数可能是5个或6个或7个.