题目内容
 如图,AB是圆O的直径,CD⊥AB于D点,AD=4cm,DB=9cm,求CB的长.
如图,AB是圆O的直径,CD⊥AB于D点,AD=4cm,DB=9cm,求CB的长.考点:相似三角形的判定与性质,圆周角定理
专题:计算题
分析:连结AC,根据圆周角定理由AB是圆O的直径得到∠ACB=90°,由CD⊥AB得到∠CDA=90°,再根据等角的余角相等得到∠ACD=∠B,则根据三角形相似的判定方法得到Rt△ACD∽Rt△CBD,利用相似比可计算出CD=6,然后在Rt△BCD中,根据勾股定理计算CB.
解答:解:连结AC,如图,
∵AB是圆O的直径,
∴∠ACB=90°,
∴∠A+∠B=90°,
∵CD⊥AB,
∴∠CDA=90°,
∴∠A+∠ACD=90°,
∴∠ACD=∠B,
∴Rt△ACD∽Rt△CBD,
∴CD:AD=BD:CD,即CD:4=9:CD,即得CD=6,
在Rt△BCD中,CB=
=
=3
(cm).

∵AB是圆O的直径,
∴∠ACB=90°,
∴∠A+∠B=90°,
∵CD⊥AB,
∴∠CDA=90°,
∴∠A+∠ACD=90°,
∴∠ACD=∠B,
∴Rt△ACD∽Rt△CBD,
∴CD:AD=BD:CD,即CD:4=9:CD,即得CD=6,
在Rt△BCD中,CB=
| CD2+BD2 |
| 62+92 |
| 13 |
点评:本题考查了相似三角形的判定与性质:有两组角对应相等的两个三角形相似;相似三角形对应边的比相等,都等于相似比.

练习册系列答案
相关题目
下列说法正确的是( )
A、一个游戏的中奖概率是
| ||||
| B、为了解深圳中学生的心理健康情况,应该采用普查的方式 | ||||
| C、事件“小明今年中考数学考95分”是可能事件 | ||||
D、若甲组数据的方差S
|

 如图,游客从某旅游景区的景点A处下山至C处有两种路径,一中是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客同时从A处下山,甲沿AC匀速步行,速度为45m/min.乙开始从A乘缆车到B,在B处停留5min后,再从B匀速步行到C,两人同时到达.已知缆车匀速直线运动的速度为180m/min,山路AC长为2430m,经测量,∠CAB=45°,∠CBA=105°.(参考数据:
如图,游客从某旅游景区的景点A处下山至C处有两种路径,一中是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客同时从A处下山,甲沿AC匀速步行,速度为45m/min.乙开始从A乘缆车到B,在B处停留5min后,再从B匀速步行到C,两人同时到达.已知缆车匀速直线运动的速度为180m/min,山路AC长为2430m,经测量,∠CAB=45°,∠CBA=105°.(参考数据:
 如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).
如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).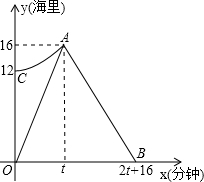 我市某海域内有一艘渔船发主障,海事救援船接到求救信号后立即从港口出发沿直线匀速前往救援,与故障船会合后立即将其拖回,如图,折线段O-A-B表示救援船在整个过程中离港口的距离y(海里)随航行时间x(分钟)的变化规律,抛物线y=ax2+k表示故障渔船在漂移过程中离港口的距离y(海里)随漂移时间x(分钟)的变化规律,已知救援船返程速度是前往速度的
我市某海域内有一艘渔船发主障,海事救援船接到求救信号后立即从港口出发沿直线匀速前往救援,与故障船会合后立即将其拖回,如图,折线段O-A-B表示救援船在整个过程中离港口的距离y(海里)随航行时间x(分钟)的变化规律,抛物线y=ax2+k表示故障渔船在漂移过程中离港口的距离y(海里)随漂移时间x(分钟)的变化规律,已知救援船返程速度是前往速度的