题目内容
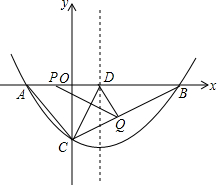 已知抛物线 y=ax2+bx+c(a>0)的图象经过过点B(12,0)和C(0,6),对称轴方程为x=2.
已知抛物线 y=ax2+bx+c(a>0)的图象经过过点B(12,0)和C(0,6),对称轴方程为x=2.(1)求该抛物线的解析式;
(2)点D在线段AB上且AD=AC,求tan∠ACD的值;
(3)若动点P从A出发沿线段AB以每秒1个单位长度速度匀速运动,同时另一动点Q以某一速度从C出发沿线段CB匀速运动,问是否在某一时刻,使线段PQ被直线CD垂直平分?若存在,请求出此时的时间t(秒)和点Q的运动速度;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)利用待定系数法求得二次函数的解析式即可;
(2)根据点D在线段AB上,且AD=AC得到点D在对称轴上,然后根据点B (12,0)和点A关于直线x=2对称、点A (-8,0),D(2,0),AD=10,AO=8、
(3)设直线CD垂直平分PQ,连接DQ,利用∠PDC=∠QDC,PD=DQ和∠ACD=∠ADC得到∠ACD=∠QDC,从而得到t=5÷1=5(秒),进一步得到存在t=5(秒)时,线段PQ被直线CD垂直平分,然后利用时间、速度、路程之间的关系求得点Q的运动速度.
(2)根据点D在线段AB上,且AD=AC得到点D在对称轴上,然后根据点B (12,0)和点A关于直线x=2对称、点A (-8,0),D(2,0),AD=10,AO=8、
(3)设直线CD垂直平分PQ,连接DQ,利用∠PDC=∠QDC,PD=DQ和∠ACD=∠ADC得到∠ACD=∠QDC,从而得到t=5÷1=5(秒),进一步得到存在t=5(秒)时,线段PQ被直线CD垂直平分,然后利用时间、速度、路程之间的关系求得点Q的运动速度.
解答:解:(1)∵抛物线经过点C(0,-6),
∴C=-6,即y=ax2+bx-6.
由y=
解得 a=
,b=-
.
∴抛物线的解析式为y=
x2-
x-6.
(2)OC=6,得到在Rt△AOC中,AC=10,然后利用锐角三角函数的性质求得结果.
点D在线段AB上,且AD=AC,∴点D在对称轴上.
点B (12,0)和点A关于直线x=2对称.
点A (-8,0),D(2,0),AD=10,AO=8,OC=6,
在Rt△AOC中,AC=
=10.
∵AD=AC,∴∠ACD=∠ADC.
∴Rt△COD中,tan∠ODC=
=
=3,
∴tan∠ACD=3.
(3)存在
设直线CD垂直平分PQ,连接DQ,
显然∠PDC=∠QDC,PD=DQ.
由(2)∠ACD=∠ADC,∴∠ACD=∠QDC,
∴DQ∥AC.
∵点D是线段AB的中点,∴DQ为中位线,
∴DQ=
AC=5.
∴AP=AD-PD=AD-DQ=10-5=5,
∴t=5÷1=5(秒),
∴存在t=5(秒)时,线段PQ被直线CD垂直平分,
此时,在Rt△BOC中,BC=
=6
.
DQ为△ABC的中位线,∴CQ=3
.
∴点Q的运动速度为每秒
个单位长度.
∴C=-6,即y=ax2+bx-6.
由y=
|
解得 a=
| 1 |
| 16 |
| 1 |
| 4 |
∴抛物线的解析式为y=
| 1 |
| 16 |
| 1 |
| 4 |
(2)OC=6,得到在Rt△AOC中,AC=10,然后利用锐角三角函数的性质求得结果.
点D在线段AB上,且AD=AC,∴点D在对称轴上.
点B (12,0)和点A关于直线x=2对称.
点A (-8,0),D(2,0),AD=10,AO=8,OC=6,
在Rt△AOC中,AC=
| AO2+OC2 |
∵AD=AC,∴∠ACD=∠ADC.
∴Rt△COD中,tan∠ODC=
| OC |
| OD |
| 6 |
| 2 |
∴tan∠ACD=3.
(3)存在
设直线CD垂直平分PQ,连接DQ,
显然∠PDC=∠QDC,PD=DQ.
由(2)∠ACD=∠ADC,∴∠ACD=∠QDC,
∴DQ∥AC.
∵点D是线段AB的中点,∴DQ为中位线,
∴DQ=
| 1 |
| 2 |
∴AP=AD-PD=AD-DQ=10-5=5,
∴t=5÷1=5(秒),
∴存在t=5(秒)时,线段PQ被直线CD垂直平分,
此时,在Rt△BOC中,BC=
| 62+122 |
| 5 |
DQ为△ABC的中位线,∴CQ=3
| 5 |
∴点Q的运动速度为每秒
3
| ||
| 5 |
点评:本题是二次函数的综合题型,其中涉及到的知识点有抛物线的顶点公式和三角形的面积求法.在求有关动点问题时要注意分析题意分情况讨论结果.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目

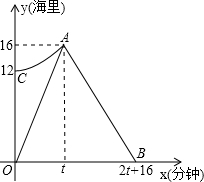 我市某海域内有一艘渔船发主障,海事救援船接到求救信号后立即从港口出发沿直线匀速前往救援,与故障船会合后立即将其拖回,如图,折线段O-A-B表示救援船在整个过程中离港口的距离y(海里)随航行时间x(分钟)的变化规律,抛物线y=ax2+k表示故障渔船在漂移过程中离港口的距离y(海里)随漂移时间x(分钟)的变化规律,已知救援船返程速度是前往速度的
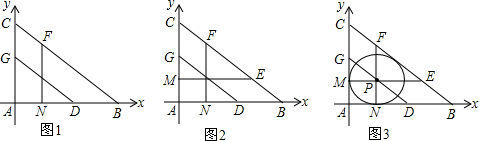
我市某海域内有一艘渔船发主障,海事救援船接到求救信号后立即从港口出发沿直线匀速前往救援,与故障船会合后立即将其拖回,如图,折线段O-A-B表示救援船在整个过程中离港口的距离y(海里)随航行时间x(分钟)的变化规律,抛物线y=ax2+k表示故障渔船在漂移过程中离港口的距离y(海里)随漂移时间x(分钟)的变化规律,已知救援船返程速度是前往速度的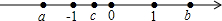 实数a、b、c,如图,化简
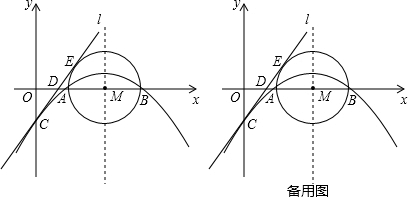
实数a、b、c,如图,化简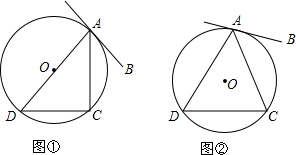 如图,直线AB切⊙O于点A,点C、D在⊙O上.试探求:
如图,直线AB切⊙O于点A,点C、D在⊙O上.试探求: