题目内容
 如图,点O为∠APB角平分线上一点,半径为2的⊙O切PA于A点,AP=4.
如图,点O为∠APB角平分线上一点,半径为2的⊙O切PA于A点,AP=4.(1)求证:PB是⊙O的切线;
(2)若连接两切点交OP于点C,△APC沿AC翻折AP的对应线段AQ交⊙O于点E,求AE的长.
考点:切线的判定与性质,翻折变换(折叠问题)
专题:
分析:(1)根据题意得出△PAO≌△PBO(AAS),进而得出AO=BO,∠PBO=∠PAO=90°,求出即可;
(2)首先利用勾股定理以及三角形面积AC,CO的长,即可得出FQ以及AE的长.
(2)首先利用勾股定理以及三角形面积AC,CO的长,即可得出FQ以及AE的长.
解答: (1)证明:过点O作OB⊥PB,连接AO,
(1)证明:过点O作OB⊥PB,连接AO,
∵PA是⊙O的切线,
∴OA⊥PA,
在△PAO和△PBO中
,
∴△PAO≌△PBO(AAS),
∴AO=BO,∠PBO=∠PAO=90°,
∴PB是⊙O的切线;
(2)解:∵∠PAO=90°,AO=2,PA=4,
∴PO=2
,
∵PA,PB是⊙O的切线,∠APO=∠OPB,
∴PA=PB,PC⊥AB,
∴AC×PO=AO×PA,
∴AC=
=
,
∴tan∠APO=
=
,
∵∠APO=∠Q,
∴CQ=2×AC=
,
∵AO=2,
∴CO=
=
,
∴FQ=
-2-
=
-2,
∴NQ=
-2+4=
+2,
∵EQ×AQ=FQ×QN,
∴设AE=x,则4(4-x)=(
-2)×(
+2)
解得:x=
,
即AE的长为
.
 (1)证明:过点O作OB⊥PB,连接AO,
(1)证明:过点O作OB⊥PB,连接AO,∵PA是⊙O的切线,
∴OA⊥PA,
在△PAO和△PBO中
|
∴△PAO≌△PBO(AAS),
∴AO=BO,∠PBO=∠PAO=90°,
∴PB是⊙O的切线;
(2)解:∵∠PAO=90°,AO=2,PA=4,
∴PO=2
| 5 |
∵PA,PB是⊙O的切线,∠APO=∠OPB,
∴PA=PB,PC⊥AB,
∴AC×PO=AO×PA,
∴AC=
| 2×4 | ||
2
|
4
| ||
| 5 |
∴tan∠APO=
| AO |
| AP |
| 1 |
| 2 |
∵∠APO=∠Q,
∴CQ=2×AC=
8
| ||
| 5 |
∵AO=2,
∴CO=
| AO2-AC2 |
2
| ||
| 5 |
∴FQ=
8
| ||
| 5 |
2
| ||
| 5 |
6
| ||
| 5 |
∴NQ=
6
| ||
| 5 |
6
| ||
| 5 |
∵EQ×AQ=FQ×QN,
∴设AE=x,则4(4-x)=(
6
| ||
| 5 |
6
| ||
| 5 |
解得:x=
| 16 |
| 5 |
即AE的长为
| 16 |
| 5 |
点评:此题主要考查了勾股定理以及锐角三角函数关系以及切线的判定与性质等知识,熟练利用切割线定理推论得出是解题关键.

练习册系列答案
相关题目
 如图,游客从某旅游景区的景点A处下山至C处有两种路径,一中是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客同时从A处下山,甲沿AC匀速步行,速度为45m/min.乙开始从A乘缆车到B,在B处停留5min后,再从B匀速步行到C,两人同时到达.已知缆车匀速直线运动的速度为180m/min,山路AC长为2430m,经测量,∠CAB=45°,∠CBA=105°.(参考数据:
如图,游客从某旅游景区的景点A处下山至C处有两种路径,一中是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客同时从A处下山,甲沿AC匀速步行,速度为45m/min.乙开始从A乘缆车到B,在B处停留5min后,再从B匀速步行到C,两人同时到达.已知缆车匀速直线运动的速度为180m/min,山路AC长为2430m,经测量,∠CAB=45°,∠CBA=105°.(参考数据: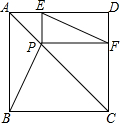 如图,已知P是正方形ABCD对角线AC上的一点,不与A,C重合,PE⊥DA,PF⊥CD,E、F为垂足,
如图,已知P是正方形ABCD对角线AC上的一点,不与A,C重合,PE⊥DA,PF⊥CD,E、F为垂足, 如图,在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧
如图,在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧
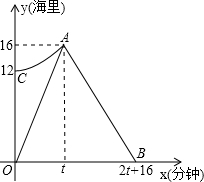 我市某海域内有一艘渔船发主障,海事救援船接到求救信号后立即从港口出发沿直线匀速前往救援,与故障船会合后立即将其拖回,如图,折线段O-A-B表示救援船在整个过程中离港口的距离y(海里)随航行时间x(分钟)的变化规律,抛物线y=ax2+k表示故障渔船在漂移过程中离港口的距离y(海里)随漂移时间x(分钟)的变化规律,已知救援船返程速度是前往速度的
我市某海域内有一艘渔船发主障,海事救援船接到求救信号后立即从港口出发沿直线匀速前往救援,与故障船会合后立即将其拖回,如图,折线段O-A-B表示救援船在整个过程中离港口的距离y(海里)随航行时间x(分钟)的变化规律,抛物线y=ax2+k表示故障渔船在漂移过程中离港口的距离y(海里)随漂移时间x(分钟)的变化规律,已知救援船返程速度是前往速度的 如图,已知AD是∠BAC的平分线,在不添加任何辅助线的前提下,要使△AED≌△AFD,还需添加一个条件,这个条件可以是
如图,已知AD是∠BAC的平分线,在不添加任何辅助线的前提下,要使△AED≌△AFD,还需添加一个条件,这个条件可以是