题目内容
10.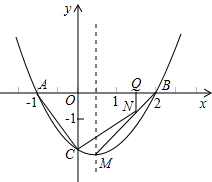 已知抛物线如图所示.
已知抛物线如图所示.(1)求抛物线的解析式及抛物线顶点M的坐标;
(2)若点N为线段BM上一点,过点N作x轴的垂线,垂足为点Q,当点N在线段BM上运动时(点N不与点B、点M重合),设OQ的长为t,四边形NQAC的面积为S,求S与t之间的函数关系式及自变量t的取值范围.
分析 (1)根据题意设出抛物线的交点式,代入与y轴的一个交点(0,-2),可确定解析式.
(2)根据B、M两点的坐标可以求得直线BM的解析式y=3x-6;由该解析式可以求得NQ=6-3t;根据图形可知S四边形NQAC=S梯形QNCO+S△AOC.
解答 解:(1)设抛物线解析式为:y=a(x+1)(x-2),
将点(0,-2)代入,得:-2=-2a,
解得:a=1,
故抛物线解析式为:y=(x+1)(x-2).
因为y=(x+1)(x-2)=x2-x-2=(x-$\frac{1}{2}$)2-$\frac{9}{4}$,
所以抛物线顶点M的坐标为($\frac{1}{2}$,-$\frac{9}{4}$).
(2)根据B(2,0)、M($\frac{1}{2}$,-$\frac{9}{4}$);
易知直线BM的解析式为y=$\frac{3}{2}$x-3;
∵当x=t时,y=$\frac{3}{2}$t-3;
∴NQ=3-$\frac{3}{2}$t;
∴S四边形NQAC=S梯形QNCO+S△AOC=$\frac{1}{2}$×(2+3-$\frac{3}{2}$t)×t+$\frac{1}{2}$×2×1,即S四边形PQAC=-$\frac{3}{4}$t2+$\frac{5}{2}$t+1($\frac{1}{2}$<t<2).
点评 本题考查了待定系数法求抛物线的解析式,直线的解析式,梯形的面积和三角形面积等,待定系数法是本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

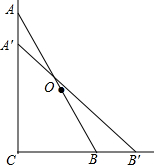 如图,一架梯子AB长2.5m,顶端A靠在墙AC上,此时,梯子下端B与墙角C距离为1.5m,现梯子滑动后停在A′B′的位置上,测得BB′长为0.5m.
如图,一架梯子AB长2.5m,顶端A靠在墙AC上,此时,梯子下端B与墙角C距离为1.5m,现梯子滑动后停在A′B′的位置上,测得BB′长为0.5m.