题目内容
9.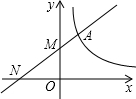 如图,一次函数y=kx+2与反比例函数y=$\frac{4}{x}$(x>0)的图象交于点A,与y轴交于点M,与x轴交于点N,且AM:MN=1:2,则k=$\frac{3}{4}$.
如图,一次函数y=kx+2与反比例函数y=$\frac{4}{x}$(x>0)的图象交于点A,与y轴交于点M,与x轴交于点N,且AM:MN=1:2,则k=$\frac{3}{4}$.
分析 利用相似三角形的判定与性质得出A点坐标,进而代入一次函数解析式得出答案.
解答 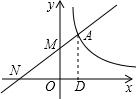 解:过点A作AD⊥x轴,
解:过点A作AD⊥x轴,
由题意可得:MO∥AO,
则△NOM∽△NDA,
∵AM:MN=1:2,
∴$\frac{NM}{AN}$=$\frac{MO}{AD}$=$\frac{2}{3}$,
∵一次函数y=kx+2,与y轴交点为;(0,2),
∴MO=2,
∴AD=3,
∴y=3时,3=$\frac{4}{x}$,
解得:x=$\frac{4}{3}$,
∴A($\frac{4}{3}$,3),将A点代入y=kx+2得:
3=$\frac{4}{3}$k+2,
解得:k=$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 此题主要考查了反比例函数与一次函数交点问题以及相似三角形的判定与性质等知识,得出A点坐标是解题关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
4.下列事件属于必然事件的是( )
| A. | 蒙上眼睛射击正中靶心 | |
| B. | 买一张彩票一定中奖 | |
| C. | 打开电视机,电视正在播放新闻联播 | |
| D. | 月球绕着地球转 |
18.式子2$\sqrt{3}$+$\sqrt{2}$的结果精确到0.01为(可用计算器计算或笔算)( )
| A. | 4.9 | B. | 4.87 | C. | 4.88 | D. | 4.89 |
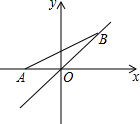 如图,定点A(-2,0),动点B在直线y=x上运动,当线段AB最短时,点B的坐标为(-1,-1).
如图,定点A(-2,0),动点B在直线y=x上运动,当线段AB最短时,点B的坐标为(-1,-1).