题目内容
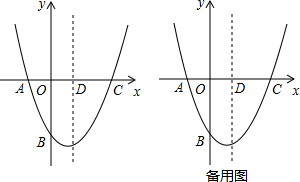
19.如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(-1,0),B(0,-$\sqrt{3}$),C(2,0),其对称轴与x轴交于点D(1)求二次函数的表达式及其顶点坐标;
(2)若P为y轴上的一个动点,连接PD,则$\frac{1}{2}$PB+PD的最小值为$\frac{3\sqrt{3}}{4}$;
(3)M(x,t)为抛物线对称轴上一动点
①若平面内存在点N,使得以A,B,M,N为顶点的四边形为菱形,则这样的点N共有5个;
②连接MA,MB,若∠AMB不小于60°,求t的取值范围.
分析 (1)利用待定系数法转化为解方程组解决问题.
(2)如图1中,连接AB,作DH⊥AB于H,交OB于P,此时$\frac{1}{2}$PB+PD最小.最小值就是线段DH,求出DH即可.
(3)①先在对称轴上寻找满足△ABM是等腰三角形的点M,由此即可解决问题.
②作AB的中垂线与y轴交于点E,连接EA,则∠AEB=120°,以E为圆心,EB为半径作圆,与抛物线对称轴交于点F、G.则∠AFB=∠AGB=60°,从而线段FG上的点满足题意,求出F、G的坐标即可解决问题.
解答 解:(1)由题意$\left\{\begin{array}{l}{a-b+c=0}\\{c=-\sqrt{3}}\\{4a+2b+c=0}\end{array}\right.$解得$\left\{\begin{array}{l}{a=\frac{\sqrt{3}}{2}}\\{b=-\frac{\sqrt{3}}{2}}\\{c=-\sqrt{3}}\end{array}\right.$,
∴抛物线解析式为y=$\frac{\sqrt{3}}{2}$x2-$\frac{\sqrt{3}}{2}$x-$\sqrt{3}$,
∵y=$\frac{\sqrt{3}}{2}$x2-$\frac{\sqrt{3}}{2}$x-$\sqrt{3}$=$\frac{\sqrt{3}}{2}$(x-$\frac{1}{2}$)2-$\frac{9\sqrt{3}}{8}$,
∴顶点坐标($\frac{1}{2}$,-$\frac{9\sqrt{3}}{8}$).
(2)如图1中,连接AB,作DH⊥AB于H,交OB于P,
此时$\frac{1}{2}$PB+PD最小.
理由:∵OA=1,OB=$\sqrt{3}$,
∴tan∠ABO=$\frac{OA}{OB}$=$\frac{\sqrt{3}}{3}$,
∴∠ABO=30°,
∴PH=$\frac{1}{2}$PB,
∴$\frac{1}{2}$PB+PD=PH+PD=DH,
∴此时$\frac{1}{2}$PB+PD最短(垂线段最短).
在RT△ADH中,∵∠AHD=90°,AD=$\frac{3}{2}$,∠HAD=60°,
∴sin60°=$\frac{DH}{AD}$,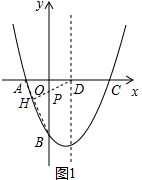
∴DH=$\frac{3\sqrt{3}}{4}$,
∴$\frac{1}{2}$PB+PD的最小值为$\frac{3\sqrt{3}}{4}$.
故答案为$\frac{3\sqrt{3}}{4}$.
(3)①以A为圆心AB为半径画弧与对称轴有两个交点,
以B为圆心AB为半径画弧与对称轴也有两个交点,
线段AB的垂直平分线与对称轴有一个交点,
所以满足条件的点M有5个,即满足条件的点N也有5个,
故答案为5.
②如图,RT△AOB中,∵tan∠ABO=$\frac{OA}{OB}$=$\frac{\sqrt{3}}{3}$,
∴∠ABO=30°,
作AB的中垂线与y轴交于点E,连接EA,则∠AEB=120°,
以E为圆心,EB为半径作圆,与抛物线对称轴交于点F、G.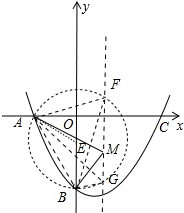
则∠AFB=∠AGB=60°,从而线段FG上的点满足题意,
∵EB=$\frac{\frac{AB}{2}}{cos30°}$=$\frac{2\sqrt{3}}{3}$,
∴OE=OB-EB=$\frac{\sqrt{3}}{3}$,
∵F($\frac{1}{2}$,t),EF2=EB2,
∴($\frac{1}{2}$)2+(t+$\frac{\sqrt{3}}{3}$)2=($\frac{2\sqrt{3}}{3}$)2,
解得t=$\frac{-2\sqrt{3}+\sqrt{39}}{6}$或$\frac{-2\sqrt{3}-\sqrt{39}}{6}$,
故F($\frac{1}{2}$,$\frac{-2\sqrt{3}+\sqrt{39}}{6}$),G($\frac{1}{2}$,$\frac{-2\sqrt{3}-\sqrt{39}}{6}$),
∴t的取值范围$\frac{-2\sqrt{3}-\sqrt{39}}{6}$≤t≤$\frac{-2\sqrt{3}+\sqrt{39}}{6}$
点评 本题考查二次函数综合题、锐角三角函数、最短问题、圆等知识,解题的关键是掌握待定系数法确定函数解析式,学会利用垂线段最短解决实际问题中的最短问题,学会添加辅助线,构造圆解决角度问题,属于中考压轴题.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| A. | 3$\sqrt{\frac{1}{3}}$=$\sqrt{3}$ | B. | $\sqrt{2}$$+\sqrt{3}$=$\sqrt{5}$ | C. | 3+2$\sqrt{2}$=5$\sqrt{2}$ | D. | -$\sqrt{(-2)^{2}}$=2 |
| A. | $\frac{x}{2}$ | B. | $\frac{1}{3}{x}^{2}$ | C. | $\frac{2x+1}{x-3}$ | D. | $\frac{x}{π-2}$ |
| A. | 了解全国中学生的视力情况 | |
| B. | 调查某批次日光灯的使用寿命 | |
| C. | 调查市场上矿泉水的质量情况 | |
| D. | 调查机场乘坐飞机的旅客是否携带了违禁物品 |