题目内容
7.下列计算正确的是( )| A. | 3$\sqrt{\frac{1}{3}}$=$\sqrt{3}$ | B. | $\sqrt{2}$$+\sqrt{3}$=$\sqrt{5}$ | C. | 3+2$\sqrt{2}$=5$\sqrt{2}$ | D. | -$\sqrt{(-2)^{2}}$=2 |
分析 分别根据二次根式的化简法则、合并同类项的法则对各选项进行逐一分析即可.
解答 解:A、3$\sqrt{\frac{1}{3}}$=$\sqrt{3}$,故本选项正确;
B、$\sqrt{2}$与$\sqrt{3}$不是同类项,不能合并,故本选项错误;
C、3与2$\sqrt{2}$不是同类项,不能合并,故本选项错误;
D、-$\sqrt{(-2)^{2}}$=-2≠2,故本选项错误.
故选A.
点评 本题考查的是二次根式的加减法,熟知二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变是解答此题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
18.下列多项式中,能分解因式的是( )
| A. | x2+2x | B. | x2-y | C. | x2+y2 | D. | x2-xy+y2 |
15.不等式2x+1≤5的解集,在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
17.把$\sqrt{\frac{1}{32}}$化成最简二次根式为( )
| A. | 32$\sqrt{32}$ | B. | $\frac{1}{32}$$\sqrt{2}$ | C. | $\frac{1}{8}$$\sqrt{2}$ | D. | $\frac{1}{4}$$\sqrt{2}$ |
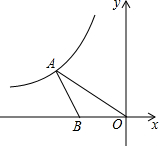 如图,在平面直角坐标系中,点A在第二象限内,点B在x轴上,∠AOB=30°,AB=BO,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点A,若S△ABO=$\sqrt{3}$,则k的值为-3$\sqrt{3}$.
如图,在平面直角坐标系中,点A在第二象限内,点B在x轴上,∠AOB=30°,AB=BO,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点A,若S△ABO=$\sqrt{3}$,则k的值为-3$\sqrt{3}$.