题目内容
10.矩形ABCD中,AB=5,BC=6,点E为AD上一个动点,将△ABE沿折线BE折叠后得到△GBE,延长BG交矩形一边于F点,若点F恰好为该边的中点,则此时AE的长为$\frac{5\sqrt{34}-25}{3}$或$\frac{10}{3}$.分析 根据对折的性质,得出AE=EG,AB=BG,然后根据勾股定理求得BF,设AE=x,再表示出EG、ED和EF,然后利用勾股定理得到关于x的方程,解方程即可求得.
解答 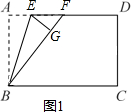 解:当F点在AD上时,如图1,
解:当F点在AD上时,如图1,
∵矩形ABCD中,AB=5,BC=6,
∴DC=AB=5,AD=BC=6,
∵点F恰好为该边的中点,
∴AF=FD=3,
∴BF=$\sqrt{A{F}^{2}+A{B}^{2}}$=$\sqrt{{3}^{2}+{5}^{2}}$=$\sqrt{34}$,
∵BG=AB=5,
∴GF=$\sqrt{34}$-5,
∵∠BGE=∠A=90°,
∴EG2+GF2=EF2,
设AE=x,则EF=3-x,
∵EG=AE=x,
∴x2+($\sqrt{34}$-5)2=(3-x)2,
解得x=$\frac{5\sqrt{34}-25}{3}$,
当F点在CD上时,如图2,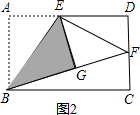
∵矩形ABCD中,AB=5,BC=6,
∴DC=AB=5,AD=BC=6,
∵点F恰好为该边的中点,
∴DF=CF=2.5,
∴BF=$\sqrt{B{C}^{2}+C{F}^{2}}$=$\sqrt{{6}^{2}+2.{5}^{2}}$=$\frac{13}{2}$,
∵BG=AB=5,
∴GF=6.5-5=1.5,
∵∠BGE=∠A=90°,
∴EG2+GF2=ED2+DF2,
设AE=x,则ED=6-x,
∵EG=AE=x,
∴x2+1.52=(6-x)2+2.52,
解得x=$\frac{10}{3}$,
∴AE=$\frac{10}{3}$,
综上,AE的长为$\frac{5\sqrt{34}-25}{3}$或$\frac{10}{3}$,
故答案为$\frac{5\sqrt{34}-25}{3}$或$\frac{10}{3}$.
点评 此题考查了矩形的判定与性质、折叠的性质、勾股定理的应用.此题难度适中,注意数形结合思想的应用.

 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案| A. | x2+2x | B. | x2-y | C. | x2+y2 | D. | x2-xy+y2 |
| A. |  | B. |  | C. |  | D. |  |
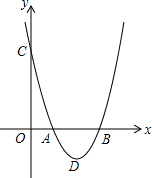 如图,二次函数y=a(x2-4x+3)(a>0)的图象与x轴交于A、B两点,与y轴交于点C,点D是抛物线的顶点
如图,二次函数y=a(x2-4x+3)(a>0)的图象与x轴交于A、B两点,与y轴交于点C,点D是抛物线的顶点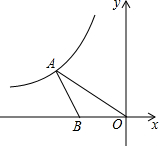 如图,在平面直角坐标系中,点A在第二象限内,点B在x轴上,∠AOB=30°,AB=BO,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点A,若S△ABO=$\sqrt{3}$,则k的值为-3$\sqrt{3}$.
如图,在平面直角坐标系中,点A在第二象限内,点B在x轴上,∠AOB=30°,AB=BO,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点A,若S△ABO=$\sqrt{3}$,则k的值为-3$\sqrt{3}$.