题目内容
12.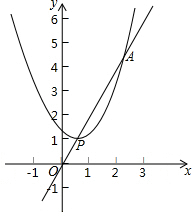 如图,抛物线y=(x-m)2+n的顶点P在直线y=2x上,该抛物线与直线的另一个交点为A,与y轴的交点为Q.
如图,抛物线y=(x-m)2+n的顶点P在直线y=2x上,该抛物线与直线的另一个交点为A,与y轴的交点为Q.(1)当m=n-1时,求m的值;
(2)当AQ∥x轴时,试确定抛物线的解析式;
(3)随着顶点P在直线y=2x上的运动,是否存在直角△PAQ?若存在,请直接写出点P的坐标;若不存在,说明理由.
分析 (1)由抛物线的顶点在y=2x上可知n=2m,然后由m=n-1可求得m的值;
(2)先求得点Q、点A的坐标(用含m的式子表示),然后根据平行与x轴的直线上所有点的纵坐标相等列出关于m的方程,从而可求得m的值;
(3)先求得直线AQ、PQ的一次项系数“k”的值(用含m的式子表示),然后依据相互垂直的两条直线的一次项系数的乘积是-1,分别列出关m的方程求解即可.
解答 解:(1)∵抛物线的解析式为y=(x-m)2+n,
∴P(m,n).
∵顶点P在直线y=2x上,
∴n=2m.
又∵m=n-1,
∴m=2m-1.
解得:m=1.
(2)∵n=2m,
∴抛物线的解析式为y=(x-m)2+2m.
∵当x=0时,y=m2+2m,
∴点Q的坐标为(0,m2+2m).
由y=(x-m)2+2m与y=2x得:2x=(x-m)2+2m,解得:x1=m,x2=m+2.
当x=m时,y=2m,即点P的坐标为(m,2m),
当x=m+2时,y=2m+4,即点A的坐标为(m+2,2m+4).
∵AQ∥x轴,
∴m2+2m=2m+4,解得:m=2或m=-2.
∵当m=-2时,点A与点Q与原点重合,与AQ∥x轴不符,
∴m=-2不合题意.
∴m=2.
∴抛物线的解析式为y=(x-2)2+4.
(3)∵Q(0,m2+2m),P(m,2m),A(m+2,2m+4),
∴直线AQ的一次项系数=$\frac{2m+4-({m}^{2}+2m)}{m+2-0}$=-m+2,直线PQ的一次项系数=$\frac{2m-({m}^{2}+2m)}{m-0}$=-m.
①当∠AQP=90°时,-m(-m+2)=-1,解得m1=m2=1,则P(1,2);
②当∠APQ=90°时,-m×2=-1,解得m=$\frac{1}{2}$,则P($\frac{1}{2}$,1);
③当∠PAQ=90°时,(-m+2)×2=-1,解得m=$\frac{5}{2}$,则P($\frac{5}{2}$,5).
综上所述,点P的坐标为(1,2)或($\frac{1}{2}$,1)或P($\frac{5}{2}$,5).
点评 本题主要考查的是二次函数的综合应用,依据平行与x轴的直线上所有点的纵坐标相等、相互垂直的两条直线的一次项系数的乘积是-1列出关于m的方程是解题的关键.

 备战中考寒假系列答案
备战中考寒假系列答案| 甲 | 7 | 9 | 8 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
| 乙 | 10 | 7 | 8 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(2)计算乙队的平均成绩和方差.
(3)已知甲队的成绩的方差是1.4,则成绩较为整齐的是乙 队.
