题目内容
17. 如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=4cm.
如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=4cm.
分析 连接OA,根据垂径定理求出AC的长,根据勾股定理求出答案.
解答  解:连接OA,
解:连接OA,
∵OC⊥AB,
∴AC=$\frac{1}{2}$AB=3cm,
∴OC=$\sqrt{O{A}^{2}-A{C}^{2}}$=4(cm).
故答案是:4cm.
点评 本题考查的是垂径定理和勾股定理的应用,掌握垂直于弦的直径平分这条弦是解题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
7. 如图,圆内接四边形ABCD中,∠A=80°,若$\widehat{ABC}$、$\widehat{ADC}$的长度分别为7π,11π,则$\widehat{BAD}$的长度为( )
如图,圆内接四边形ABCD中,∠A=80°,若$\widehat{ABC}$、$\widehat{ADC}$的长度分别为7π,11π,则$\widehat{BAD}$的长度为( )
 如图,圆内接四边形ABCD中,∠A=80°,若$\widehat{ABC}$、$\widehat{ADC}$的长度分别为7π,11π,则$\widehat{BAD}$的长度为( )
如图,圆内接四边形ABCD中,∠A=80°,若$\widehat{ABC}$、$\widehat{ADC}$的长度分别为7π,11π,则$\widehat{BAD}$的长度为( )| A. | 4π | B. | 8π | C. | 10π | D. | 15π |
8.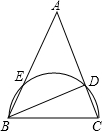 如图,在△ABC中,AB=AC,以BC为直径画半圆交AB于E,交AC于D,$\widehat{CD}$的度数为40°,则∠A的度数是( )
如图,在△ABC中,AB=AC,以BC为直径画半圆交AB于E,交AC于D,$\widehat{CD}$的度数为40°,则∠A的度数是( )
 如图,在△ABC中,AB=AC,以BC为直径画半圆交AB于E,交AC于D,$\widehat{CD}$的度数为40°,则∠A的度数是( )
如图,在△ABC中,AB=AC,以BC为直径画半圆交AB于E,交AC于D,$\widehat{CD}$的度数为40°,则∠A的度数是( )| A. | 40° | B. | 70° | C. | 50° | D. | 20° |
5.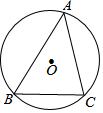 如图,⊙O是△ABC的外接圆,⊙O的半径为3,∠A=45°,则弧BC的长是( )
如图,⊙O是△ABC的外接圆,⊙O的半径为3,∠A=45°,则弧BC的长是( )
 如图,⊙O是△ABC的外接圆,⊙O的半径为3,∠A=45°,则弧BC的长是( )
如图,⊙O是△ABC的外接圆,⊙O的半径为3,∠A=45°,则弧BC的长是( )| A. | $\frac{3}{4}$π | B. | $\frac{3}{2}$ π | C. | $\frac{45}{2}$ π | D. | $\frac{9}{4}$ π |
6.下列计算正确的是( )
| A. | -5+2=-7 | B. | 6÷(-2)=-3 | C. | -7-2=9 | D. | -22=4 |
12.为了美化校园环境,争创绿色学校,某县教育局委托园林公司对A,B两校进行校园绿化,已知A校有如图(1)的阴影部分空地需铺设草坪,B校有如图(2)的阴影部分空地需铺设草坪,在甲、乙两地分别有同种草皮3500米2和2500米2出售,且售价一样,若园林公司向甲、乙两地购买草皮,其路程和运费单价表如下:
路程、运费单价表
(注:运费单价表示每平方米草皮运送1千米所需的人民币)

求:(1)分别求出图1、图2的阴影部分面积;
(2)若园林公司将甲地3500m2的草皮全部运往A校,请你求出园林公司运送草皮去A、B两校的总运费;
(3)请你给出一种运送方案,使得园林公司支付出送草皮的总运费不超过15000元.
路程、运费单价表
| A校 | B校 | |||
| 路程(千米) | 运费单价(元) | 路程(千米) | 运费单价(元) | |
| 甲地 | 20 | 0.15 | 10 | 0.15 |
| 乙地 | 15 | 0.20 | 20 | 0.20 |

求:(1)分别求出图1、图2的阴影部分面积;
(2)若园林公司将甲地3500m2的草皮全部运往A校,请你求出园林公司运送草皮去A、B两校的总运费;
(3)请你给出一种运送方案,使得园林公司支付出送草皮的总运费不超过15000元.
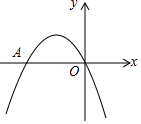 如图,二次函数y=-x2+bx+c的图象经过坐标原点,与x轴的另一个交点为A(-2,0).
如图,二次函数y=-x2+bx+c的图象经过坐标原点,与x轴的另一个交点为A(-2,0).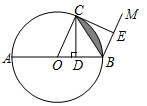 如图,⊙O的直径AB=4,C是⊙O上一点,连接OC.过点C作CD⊥AB,垂足为D,过点B作BM∥OC,在射线BM上取点E,使BE=BD,连接CE.
如图,⊙O的直径AB=4,C是⊙O上一点,连接OC.过点C作CD⊥AB,垂足为D,过点B作BM∥OC,在射线BM上取点E,使BE=BD,连接CE.