题目内容
12.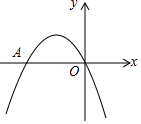 如图,二次函数y=-x2+bx+c的图象经过坐标原点,与x轴的另一个交点为A(-2,0).
如图,二次函数y=-x2+bx+c的图象经过坐标原点,与x轴的另一个交点为A(-2,0).(1)求二次函数的解析式;
(2)在抛物线上是否存在一点P,使△AOP的面积为3?若存在请求出点P的坐标,若不存在,请说明理由.
分析 (1)把点(0,0)和点A(-2,0)分别代入函数关系式来求b、c的值,可得二次函数的解析式;
(2)设点P的坐标为(x,-x2-2x).利用三角形的面积公式得到-x2-2x=±3.通过解方程来求x的值,则易求点P的坐标.
解答 解:(1)∵二次函数y=-x2+bx+c的图象经过坐标原点(0,0)
∴c=0
又∵二次函数y=-x2+bx+c的图象过点A(-2,0)
∴-(-2)2-2b+0=0,
∴b=-2,
∴所求b、c值分别为-2,0
∴y=-x2-2x,
(2)存在一点P,满足S△AOP=3.
设点P的坐标为(x,-x2-2x)
∵S△AOP=3
∴$\frac{1}{2}×2×$|-x2-2x|=3
∴-x2-2x=±3
当-x2-2x=3时,此方程无解;
当-x2-2x=-3时,解得x1=-3,x2=1,
∴点P的坐标为:(-3,-3)或(1,-3).
点评 本题考查了抛物线与x轴的交点和利用待定系数法来求抛物线的解析式,设点P的坐标为(x,-x2-2x)是解答此题的关键.

练习册系列答案
相关题目
7.化简:-$\sqrt{(1-sin52°)^{2}}$-$\sqrt{(1-tan52°)^{2}}$的结果是( )
| A. | tan52°-sin52° | B. | sin52°-tan52° | C. | 2-sin52°-tan52° | D. | -sin52°-tan52° |
7.若实数x,y满足$\frac{1}{2}$y-xy+x2+2=0,则实数y满足的条件是( )
| A. | y≤-2 | B. | y≥4 | C. | y2-2y-8≥0 | D. | 一切实数 |
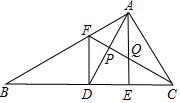 如图,D为△ABC中边BC中点,E为CD上一点,将△ACE沿AE折叠时C与D重合,F为AB上一点,FB=FC,FC与AD、AE分别交于P、Q点,下列结论
如图,D为△ABC中边BC中点,E为CD上一点,将△ACE沿AE折叠时C与D重合,F为AB上一点,FB=FC,FC与AD、AE分别交于P、Q点,下列结论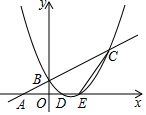 已知:如图一次函数y=$\frac{1}{2}$x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=$\frac{1}{2}$x2+bx+c的图象与一次函数y=$\frac{1}{2}$x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0)
已知:如图一次函数y=$\frac{1}{2}$x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=$\frac{1}{2}$x2+bx+c的图象与一次函数y=$\frac{1}{2}$x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0) 如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=4cm.
如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=4cm.
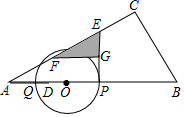 如图,在△ABC中,∠C=90°,∠CAB=30°,AB=10,点D在线段AB上,AD=2.点P,Q以相同的速度从D点同时出发,点P沿DB方向运动,点Q沿DA方向到点A后立刻以原速返回向点B运动.以PQ为直径构造⊙O,过点P作⊙O的切线交折线AC-CB于点E,将线段EP绕点E顺时针旋转60°得到EF,过F作FG⊥EP于G,当P运动到点B时,Q也停止运动,设DP=m.
如图,在△ABC中,∠C=90°,∠CAB=30°,AB=10,点D在线段AB上,AD=2.点P,Q以相同的速度从D点同时出发,点P沿DB方向运动,点Q沿DA方向到点A后立刻以原速返回向点B运动.以PQ为直径构造⊙O,过点P作⊙O的切线交折线AC-CB于点E,将线段EP绕点E顺时针旋转60°得到EF,过F作FG⊥EP于G,当P运动到点B时,Q也停止运动,设DP=m.