题目内容
已知a,b,c是Rt△ABC的三边长,△A1B1C1的三边长分别是2a,2b,2c,那么,△A1B1C1是直角三角形吗?为什么?
考点:勾股定理的逆定理,勾股定理
专题:
分析:根据勾股定理的逆定理判断即可.只需判断两边的平方之和等于第三边的平方即可.
解答:解:△A1B1C1是直角三角形,
理由:∵a,b,c是Rt△ABC的三边长,设c是斜边,
∴由勾股定理得:a2+b2=c2,
∵(2a)2+(2b)2=4a2+4b2=4(a2+b2)=4c2=(2c)2,
∴△A1B1C1是直角三角形.
理由:∵a,b,c是Rt△ABC的三边长,设c是斜边,
∴由勾股定理得:a2+b2=c2,
∵(2a)2+(2b)2=4a2+4b2=4(a2+b2)=4c2=(2c)2,
∴△A1B1C1是直角三角形.
点评:此题主要考查了勾股定理及勾股定理逆定理,解题的关键是:在应用勾股定理的逆定理时,注意是两较短边的平方和等于最长边的平方.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 如图,在△ABC上,已知点D是BC的中点,且点D在AB的垂直平分线上.求证:点D也在AC的垂直平分线上.
如图,在△ABC上,已知点D是BC的中点,且点D在AB的垂直平分线上.求证:点D也在AC的垂直平分线上. 如图,平行四边形ABCD中,AC⊥AB,AC与BD相交于O,OC=1,CD=
如图,平行四边形ABCD中,AC⊥AB,AC与BD相交于O,OC=1,CD=

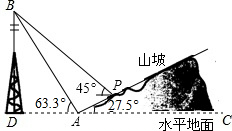 如图,某人在山脚A处测得一座塔BD的塔尖点B的仰角为63.3°,沿山坡向上走到P处再测得点B的仰角为45°,已知坡面AP=40米,坡角∠PAC=27.5°,且D、A、C在同一条直线上,求塔BD的高度(结果精确到1m)(参考数据:tan63.3°≈1.99,sin63.3°≈0.89,cos63.3°≈0.45,cos27.5°≈0.89,tan27.5°≈0.52,sin27.5°≈0.46)
如图,某人在山脚A处测得一座塔BD的塔尖点B的仰角为63.3°,沿山坡向上走到P处再测得点B的仰角为45°,已知坡面AP=40米,坡角∠PAC=27.5°,且D、A、C在同一条直线上,求塔BD的高度(结果精确到1m)(参考数据:tan63.3°≈1.99,sin63.3°≈0.89,cos63.3°≈0.45,cos27.5°≈0.89,tan27.5°≈0.52,sin27.5°≈0.46)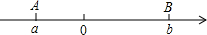 点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.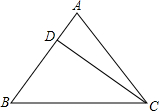 已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm,
已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm, 如图,在边长为1的小正方形组成的网络中,△ABC的三个顶点均在格点上,则cosC=
如图,在边长为1的小正方形组成的网络中,△ABC的三个顶点均在格点上,则cosC= 如图,已知∠1=∠2,∠BAD=∠BCD,证明:AD∥BC.
如图,已知∠1=∠2,∠BAD=∠BCD,证明:AD∥BC.