题目内容
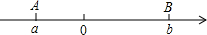 点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.回答下列问题:
(1)数轴上表示2和7两点之间的距离是
(2)数轴上表示x和-4的两点之间的距离表示为
(3)若|x-2|+|x+4|=6,则x的取值范围是
(4)若x表示一个有理数,则代数式3-2|x-2|-2|x+4|有最大值吗?若有,请求出最大值.若没有,说出理由.
考点:绝对值,数轴
专题:
分析:(1)利用题目中的已知在数轴上A、B两点之间的距离AB=|a-b|.即可得到答案;
(2)将x与-4代入|a-b|即可;
(3)根据绝对值的定义有:|x-2|+|x+4|可表示为点x到2与-4两点距离之和,当x在-4与2之间时,|x-2|+|x+4|=6,故可得x的取值范围;
(4)由代数式3-2|x-2|-2|x+4|可知,其值要想最大,则|x-2|与|x+4|的值应最小,根据绝对值的定义有:|x-2|+|x+4|可表示为点x到2与-4两点距离之和,根据几何意义分析可知:当x在-4与2之间时,|x-2|+|x+4|有最小值6,故得到代数式3-2|x-2|-2|x+4|有最大值,再将|x-2|+|x+4|的最小值6代入即可得到最大值.
(2)将x与-4代入|a-b|即可;
(3)根据绝对值的定义有:|x-2|+|x+4|可表示为点x到2与-4两点距离之和,当x在-4与2之间时,|x-2|+|x+4|=6,故可得x的取值范围;
(4)由代数式3-2|x-2|-2|x+4|可知,其值要想最大,则|x-2|与|x+4|的值应最小,根据绝对值的定义有:|x-2|+|x+4|可表示为点x到2与-4两点距离之和,根据几何意义分析可知:当x在-4与2之间时,|x-2|+|x+4|有最小值6,故得到代数式3-2|x-2|-2|x+4|有最大值,再将|x-2|+|x+4|的最小值6代入即可得到最大值.
解答:解:(1)数轴上表示2和7两点之间的距离是|7-2|=5,数轴上表示3和-3的两点之间的距离是|3-(-3)|=6;
(2)根据绝对值的定义有:数轴上表示x和-4的两点之间的距离表示为|x-(-4)|=|x+4|;
(3)|x-2|+|x+4|可表示为点x到2与-4两点距离之和,当x在-4与2之间时,|x-2|+|x+4|=6,
所以x的取值范围为:2≥x≥-4;
(4)根据绝对值的定义有:|x-2|+|x+4|可表示为点x到2与-4两点距离之和,
根据几何意义分析可知:当x在-4与2之间时,|x-2|+|x+4|有最小值6.
所以3-2|x-2|-2|x+4|=3-2(|x-2|+|x+4|)=3-12=-9.
所以代数式3-2|x-2|-2|x+4|有最大值-9.
(2)根据绝对值的定义有:数轴上表示x和-4的两点之间的距离表示为|x-(-4)|=|x+4|;
(3)|x-2|+|x+4|可表示为点x到2与-4两点距离之和,当x在-4与2之间时,|x-2|+|x+4|=6,
所以x的取值范围为:2≥x≥-4;
(4)根据绝对值的定义有:|x-2|+|x+4|可表示为点x到2与-4两点距离之和,
根据几何意义分析可知:当x在-4与2之间时,|x-2|+|x+4|有最小值6.
所以3-2|x-2|-2|x+4|=3-2(|x-2|+|x+4|)=3-12=-9.
所以代数式3-2|x-2|-2|x+4|有最大值-9.
点评:本题考查的是绝对值的定义,两点间的距离,阅读理解能力及知识的迁移能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,BE平分∠ABC,且∠1=∠3,则DE与BC平行吗?为什么?
如图,BE平分∠ABC,且∠1=∠3,则DE与BC平行吗?为什么?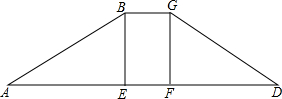 如图,水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1:3,斜坡CD的坡度i′=1:2.5.求斜坡AB的坡角α(精确到1度),坝底宽AD和斜坡AB的长(精确到0.1m)
如图,水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1:3,斜坡CD的坡度i′=1:2.5.求斜坡AB的坡角α(精确到1度),坝底宽AD和斜坡AB的长(精确到0.1m)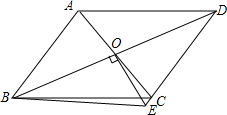 如图所示,?ABCD中,AC、BD相交于点O,OE⊥BD,交DC的延长线于E,连接BE,求证:∠ABD=∠EBD.
如图所示,?ABCD中,AC、BD相交于点O,OE⊥BD,交DC的延长线于E,连接BE,求证:∠ABD=∠EBD.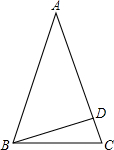 如图所示,在等腰△ABC中,AB=AC=10,点D是AC边上的一点,且CD=2,BD=6.求证:∠ADB=90°.
如图所示,在等腰△ABC中,AB=AC=10,点D是AC边上的一点,且CD=2,BD=6.求证:∠ADB=90°. 如图,AD∥EF,∠1+∠2=180°,∠1与∠BAD相等吗?为什么?
如图,AD∥EF,∠1+∠2=180°,∠1与∠BAD相等吗?为什么?