题目内容
13.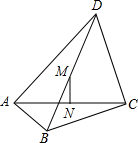 如图,在四边形ABCD中,∠BAD=∠BCD=90°,BC=12,CD=AC=16,M、N分别是对角线BD、AC的中点.
如图,在四边形ABCD中,∠BAD=∠BCD=90°,BC=12,CD=AC=16,M、N分别是对角线BD、AC的中点.(1)求证:MN⊥AC;
(2)求MN的长.
分析 (1)连接AM、CM,根据直角三角形斜边上的中线等于斜边的一半可得AM=CM=BM=DM=$\frac{1}{2}$BD,再根据等腰三角形三线合一的性质证明;
(2)利用勾股定理类似求出BD,再求出AM、AN,再利用勾股定理列式计算即可得解.
解答 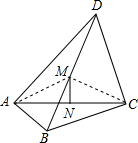 (1)证明:如图,连接AM、CM,
(1)证明:如图,连接AM、CM,
∵∠BAD=∠BCD=90°,M是BD的中点,
∴AM=CM=BM=DM=$\frac{1}{2}$BD,
∵N是AC的中点,
∴MN⊥AC;
(2)解:∵∠BCD=90°,BC=12,CD=16,
∴BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=20,
∴AM=$\frac{1}{2}$×20=10,
∵AC=16,N是AC的中点,
∴AN=$\frac{1}{2}$×16=8,
∴MN=$\sqrt{A{M}^{2}-A{N}^{2}}$=8.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形三线合一的性质,勾股定理,熟记性质与定理并作辅助线构造出等腰三角形是解题的关键.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
5.对于有理数a,b,定义一种新运算,规定a※b=-a2-b,则(-2)※(-3)=( )
| A. | 7 | B. | 1 | C. | -7 | D. | -1 |
1. 点P是直线l外一点,PO⊥l,点O为垂足,则下列结论一定成立的是( )
点P是直线l外一点,PO⊥l,点O为垂足,则下列结论一定成立的是( )
 点P是直线l外一点,PO⊥l,点O为垂足,则下列结论一定成立的是( )
点P是直线l外一点,PO⊥l,点O为垂足,则下列结论一定成立的是( )| A. | PA=PC | B. | OA=OC | C. | PO>OC | D. | PB>PO |
 已知:如图,AB∥CD,OA=OC.求证:OB=OD.
已知:如图,AB∥CD,OA=OC.求证:OB=OD. 如图,∠A=100°,∠E=25°,△ABC与△DEF关于直线l对称,则△ABC中的∠C=55°.
如图,∠A=100°,∠E=25°,△ABC与△DEF关于直线l对称,则△ABC中的∠C=55°.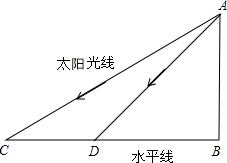 在同一时刻太阳光线与水平线的夹角是一定的.如图,有一垂直于地面的物体AB.在某一时刻太阳光线与水平线的夹角为30°时,物体AB的影长BC为4米;在另一个时刻太阳光线与水平线的夹角为45°时,则物体AB的影长BD为$\frac{4\sqrt{3}}{3}$米.(结果保留根号)
在同一时刻太阳光线与水平线的夹角是一定的.如图,有一垂直于地面的物体AB.在某一时刻太阳光线与水平线的夹角为30°时,物体AB的影长BC为4米;在另一个时刻太阳光线与水平线的夹角为45°时,则物体AB的影长BD为$\frac{4\sqrt{3}}{3}$米.(结果保留根号)