题目内容
3.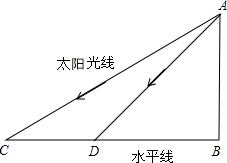 在同一时刻太阳光线与水平线的夹角是一定的.如图,有一垂直于地面的物体AB.在某一时刻太阳光线与水平线的夹角为30°时,物体AB的影长BC为4米;在另一个时刻太阳光线与水平线的夹角为45°时,则物体AB的影长BD为$\frac{4\sqrt{3}}{3}$米.(结果保留根号)
在同一时刻太阳光线与水平线的夹角是一定的.如图,有一垂直于地面的物体AB.在某一时刻太阳光线与水平线的夹角为30°时,物体AB的影长BC为4米;在另一个时刻太阳光线与水平线的夹角为45°时,则物体AB的影长BD为$\frac{4\sqrt{3}}{3}$米.(结果保留根号)
分析 根据锐角三角函数可以求得AB的长,从而可以求得BD的长,本题得以解决.
解答 解:由题意可得,
∠B=90°,BC=4,∠C=30°,
∴tan30°=$\frac{AB}{BC}=\frac{AB}{4}=\frac{\sqrt{3}}{3}$,
∴AB=$\frac{4\sqrt{3}}{3}$,
∵∠B=90°,∠ADB=45°,
∴AB=BD,
∴BD=$\frac{4\sqrt{3}}{3}$,
故答案为:$\frac{4\sqrt{3}}{3}$.
点评 本题考查解直角三角形的应用、平行投影,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
8.下列表述中,能确定准确位置的是( )
| A. | 教室第三排 | B. | 湖心南路 | ||
| C. | 南偏东40° | D. | 东经112°,北纬51° |
13. 如图,点C是线段AB的中点,点D是线段BC的中点,下列等式不正确的是( )
如图,点C是线段AB的中点,点D是线段BC的中点,下列等式不正确的是( )
 如图,点C是线段AB的中点,点D是线段BC的中点,下列等式不正确的是( )
如图,点C是线段AB的中点,点D是线段BC的中点,下列等式不正确的是( )| A. | CD=AC-DB | B. | CD=AD-BC | C. | CD=AB-AD | D. | CD=AB-BD |
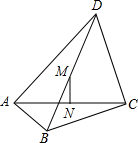 如图,在四边形ABCD中,∠BAD=∠BCD=90°,BC=12,CD=AC=16,M、N分别是对角线BD、AC的中点.
如图,在四边形ABCD中,∠BAD=∠BCD=90°,BC=12,CD=AC=16,M、N分别是对角线BD、AC的中点.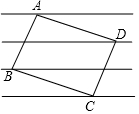 如图,矩形ABCD的四个顶点正好落在四条平行线上,并且从上到下每两条平行线间的距离都是1,如果AB:BC=3:4,那么AB的长是$\frac{\sqrt{73}}{4}$.
如图,矩形ABCD的四个顶点正好落在四条平行线上,并且从上到下每两条平行线间的距离都是1,如果AB:BC=3:4,那么AB的长是$\frac{\sqrt{73}}{4}$.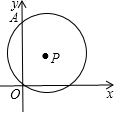 如图,点P(1,2),⊙P经过原点O,交y轴正半轴于点A,点B在⊙P上,∠BAO=45°,则点B的坐标是(3,1)或(-1,3).
如图,点P(1,2),⊙P经过原点O,交y轴正半轴于点A,点B在⊙P上,∠BAO=45°,则点B的坐标是(3,1)或(-1,3).