题目内容
小王在一次做加减消元法的练习结束之后,将
中第二个方程的两边任意乘上一个数,与第一个方程的两边分别相加,发现有一组x、y的值总是所得方程的解,连试了几次都是这样.因此他得到了一个猜想:设k是任意一个数,则方程2x+3y-5+k(x-2y+8)=0总有一个解是不变的.请找出这个固定的解,并验证、说明这个猜想的正确性.
|
考点:解二元一次方程组
专题:计算题
分析:求出方程组的解确定出固定的解,验证即可.
解答:解:
,
①-②×2得:7y=21,即y=3,
把y=3代入②得:x=-2,
∴这个固定的解为
,
当2x+3y-5=0,x-2y+8=0时,满足方程2x+3y-5+k(x-2y+8)=0总有一个解是不变的.
|
①-②×2得:7y=21,即y=3,
把y=3代入②得:x=-2,
∴这个固定的解为
|
当2x+3y-5=0,x-2y+8=0时,满足方程2x+3y-5+k(x-2y+8)=0总有一个解是不变的.
点评:此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
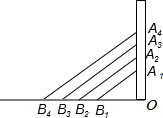 斜拉桥是我国流行的桥型之一,大跨径斜拉桥已居世界第一.如图,OA1=A1A2=A2A3=A3A4,OB1=B1B2=B2B3=B3B4,如果最长的钢索A4B4=80cm,那么钢索A2B2、A1B1的长分别是( )
斜拉桥是我国流行的桥型之一,大跨径斜拉桥已居世界第一.如图,OA1=A1A2=A2A3=A3A4,OB1=B1B2=B2B3=B3B4,如果最长的钢索A4B4=80cm,那么钢索A2B2、A1B1的长分别是( )| A、60m,40m |
| B、60m,30m |
| C、40m,20m |
| D、40m,10m |
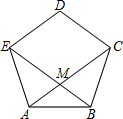 正五边形ABCDE的对角线AC、BE相交于点M.
正五边形ABCDE的对角线AC、BE相交于点M.