题目内容
5.关于x的一元二次方程x2-3x+m=0有两个不相等的实数根,则m的取值范围为m$<\frac{9}{4}$.分析 若一元二次方程有两不等根,则根的判别式△=b2-4ac>0,建立关于m的不等式,求出m的取值范围.
解答 解:∵方程有两个不相等的实数根,a=1,b=-3,c=m
∴△=b2-4ac=(-3)2-4×1×m>0,
解得m<$\frac{9}{4}$,
故答案为:m$<\frac{9}{4}$.
点评 本题考查了根的判别式,关键是掌握一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
相关题目
13.下列说法正确的是( )
| A. | 长度相等的弧叫做等弧 | B. | 半圆不是弧 | ||
| C. | 过圆心的线段是直径 | D. | 直径是弦 |
17.下列方程中,解是2的方程是( )
| A. | $\frac{2}{3}$x=2 | B. | -$\frac{1}{4}$x+$\frac{1}{2}$=0 | C. | 3x+6=0 | D. | 5-3x=1 |
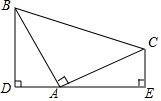 如图,△ABC是等腰直角三角形,AB=AC,CE⊥DE,BD⊥DE,若CE=2,DB=6,则DE的长为8.
如图,△ABC是等腰直角三角形,AB=AC,CE⊥DE,BD⊥DE,若CE=2,DB=6,则DE的长为8. 如图所示,AB=5cm,∠C=30°,求△ABC外接圆直径.
如图所示,AB=5cm,∠C=30°,求△ABC外接圆直径.
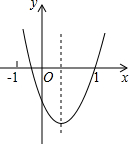 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论正确的个数是( )