如图.在△ABC中.已知AB=AC.AD平分∠BAC.点M.N分别在AB.AC边上.AM=2MB.AN=2NC．求证:DM=DN．题目和参考答案——青夏教育精英家教网—

题目内容

1．

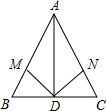如图，在△ABC中，已知AB=AC，AD平分∠BAC，点M，N分别在AB，AC边上，AM=2MB，AN=2NC．求证：DM=DN．

分析首先根据等腰三角形的性质得到AD是顶角的平分线，再利用全等三角形进行证明即可．

解答证明：∵AM=2MB，AN=2NC，AB=AC，
∴AM=AN，
∵AD平分∠BAC，
∴∠MAD=∠NAD，
在△AMD与△AND中，
$\left\{\begin{array}{l}{AM=AN}\\{∠MAD=∠NAD}\\{AD=AD}\end{array}\right.$，
∴△AMD≌△AND（SAS），
∴DM=DN．

点评本题考查了全等三角形的判定和性质，关键是根据等腰三角形的性质进行证明．

练习册系列答案

12．如图，这是台州市地图的一部分，分别以正东、正北方向为x轴、y轴的正方向建立直角坐标系，规定一个单位长度表示1km，甲、乙两人对着地图如下描述路桥区A处的位置．

则椒江区B处的坐标是（10，8$\sqrt{3}$）．

9．已知A=$\frac{{x}^{2}+2x+1}{{x}^{2}-1}$-$\frac{x}{x-1}$
（1）化简A；
（2）当x满足不等式组$\left\{\begin{array}{l}{x-1≥0}\\{x-3＜0}\end{array}\right.$，且x为整数时，求A的值．

16．

如图，△ABC中，CD是边AB上的高，且$\frac{AD}{CD}$=$\frac{CD}{BD}$．
（1）求证：△ACD∽△CBD；
（2）求∠ACB的大小．

（a³）²=a⁵

a²-2a²=-a²

13．遂宁市某生态示范园，计划种植一批核桃，原计划总产量达36万千克，为了满足市场需求，现决定改良核桃品种，改良后平均每亩产量是原计划的1.5倍，总产量比原计划增加了9万千克，种植亩数减少了20亩，则原计划和改良后平均每亩产量各多少万千克？设原计划每亩平均产量x万千克，则改良后平均每亩产量为1.5x万千克，根据题意列方程为（　　）

A．

$\frac{36}{x}$-$\frac{36+9}{1.5x}$=20

B．

$\frac{36}{x}$-$\frac{36}{1.5x}$=20

C．

$\frac{36+9}{1.5x}$-$\frac{36}{x}$=20

D．

$\frac{36}{x}$+$\frac{36+9}{1.5x}$=20

10．

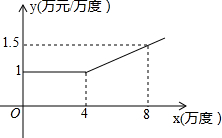某工厂在生产过程中每消耗1万度电可以产生产值5.5万元，电力公司规定，该工厂每月用电量不得超过16万度，月用电量不超过4万度时，单价是1万元/万度；超过4万度时，超过部分电量单价将按用电量进行调查，电价y与月用电量x的函数关系可用如图来表示．（效益=产值-用电量×电价）
（1）设工厂的月效益为z（万元），写出z与月用电量x（万度）之间的函数关系式，并写出自变量的取值范围；
（2）求工厂最大月效益．

11．移动互联网已经全面进入人们的日常生活．截至2015年3月，全国4G用户总数达到1.62亿，其中1.62亿用科学记数法表示为（　　）

试题分类