题目内容
10.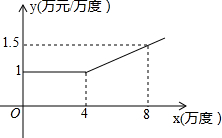 某工厂在生产过程中每消耗1万度电可以产生产值5.5万元,电力公司规定,该工厂每月用电量不得超过16万度,月用电量不超过4万度时,单价是1万元/万度;超过4万度时,超过部分电量单价将按用电量进行调查,电价y与月用电量x的函数关系可用如图来表示.(效益=产值-用电量×电价)
某工厂在生产过程中每消耗1万度电可以产生产值5.5万元,电力公司规定,该工厂每月用电量不得超过16万度,月用电量不超过4万度时,单价是1万元/万度;超过4万度时,超过部分电量单价将按用电量进行调查,电价y与月用电量x的函数关系可用如图来表示.(效益=产值-用电量×电价)(1)设工厂的月效益为z(万元),写出z与月用电量x(万度)之间的函数关系式,并写出自变量的取值范围;
(2)求工厂最大月效益.
分析 (1)根据题意知电价y与月用电量x的函数关系是分段函数,当0≤x≤4时,y=1,当4<x≤16时,函数过点(4,1)和(8,1.5)的一次函数,求出解析式;再根据效益=产值-用电量×电价,求出z与月用电量x(万度)之间的函数关系式;
(2)根据(1)中得到函数关系式,利用一次函数和二次函数的性质,求出最值.
解答 解:(1)根据题意得:电价y与月用电量x的函数关系是分段函数,
当0≤x≤4时,y=1,
当4<x≤16时,函数过点(4,1)和(8,1.5)的一次函数,
设一次函数为y=kx+b,
∴$\left\{\begin{array}{l}{4k+b=1}\\{8k+b=1.5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{8}}\\{b=\frac{1}{2}}\end{array}\right.$,
∴y=$\frac{1}{8}x+\frac{1}{2}$,
∴电价y与月用电量x的函数关系为:y=$\left\{\begin{array}{l}{1(0≤x≤4)}\\{\frac{1}{8}x+\frac{1}{2}(4<x≤16)}\end{array}\right.$
∴z与月用电量x(万度)之间的函数关系式为:z=$\left\{\begin{array}{l}{\frac{11}{2}x-x×1(0≤x≤4)}\\{\frac{11}{2}x-4×1-(x-4)(\frac{1}{8}x+\frac{1}{2})(4<x≤16}\end{array}\right.$
即z=$\left\{\begin{array}{l}{\frac{9}{2}x(0≤x≤4)}\\{-\frac{1}{8}{x}^{2}+\frac{11}{2}x-2(4<x≤16)}\end{array}\right.$
(2)当0≤x≤4时,z=$\frac{9}{2}x$
∵$\frac{9}{2}>0$,
∴z随x的增大而增大,
∴当x=4时,z有最大值,最大值为:$\frac{9}{2}×4$=18(万元);
当4<x≤16时,z=-$\frac{1}{8}{x}^{2}+\frac{11}{2}x-2$=-$\frac{1}{8}(x-22)^{2}+\frac{117}{2}$,
∵-$\frac{1}{8}<0$,
∴当x≤22时,z随x增大而增大,
16<22,则当x=16时,z最大值为54,
故当0≤x≤16时,z最大值为54,即工厂最大月效益为54万元.
点评 本题考查了一次函数的应用,解决本题的关键是图中的函数为分段函数,分别求出个函数的解析式,注意自变量的取值范围.对于最值问题,借助于一次函数的性质和二次函数的性质进行解答.

 如图是一个可以自由转动的正六边形转盘,其中三个正三角形涂有阴影,转动指针,指针落在有阴影的区域内的概率为a,如果投掷一枚硬币,正面向上的概率为b,关于a、b大小的正确判断是( )
如图是一个可以自由转动的正六边形转盘,其中三个正三角形涂有阴影,转动指针,指针落在有阴影的区域内的概率为a,如果投掷一枚硬币,正面向上的概率为b,关于a、b大小的正确判断是( )| A. | a>b | B. | a=b | C. | a<b | D. | 不能判断 |
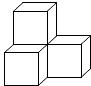 如图是由四个相同小正方体摆成的立体图形,它的俯视图是( )
如图是由四个相同小正方体摆成的立体图形,它的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
| A. | 2a+3b=5ab | B. | 5a-2a=3a | C. | a2•a3=a6 | D. | (a+b)2=a2+b2 |



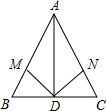 如图,在△ABC中,已知AB=AC,AD平分∠BAC,点M,N分别在AB,AC边上,AM=2MB,AN=2NC.求证:DM=DN.
如图,在△ABC中,已知AB=AC,AD平分∠BAC,点M,N分别在AB,AC边上,AM=2MB,AN=2NC.求证:DM=DN. 如图,A、B、C三点在⊙O上,且∠AOB=70°,则∠C=35度.
如图,A、B、C三点在⊙O上,且∠AOB=70°,则∠C=35度.