题目内容
9.已知A=$\frac{{x}^{2}+2x+1}{{x}^{2}-1}$-$\frac{x}{x-1}$(1)化简A;
(2)当x满足不等式组$\left\{\begin{array}{l}{x-1≥0}\\{x-3<0}\end{array}\right.$,且x为整数时,求A的值.
分析 (1)根据分式四则混合运算的运算法则,把A式进行化简即可.
(2)首先求出不等式组的解集,然后根据x为整数求出x的值,再把求出的x的值代入化简后的A式进行计算即可.
解答 解:(1)A=$\frac{{x}^{2}+2x+1}{{x}^{2}-1}$-$\frac{x}{x-1}$
=$\frac{{(x+1)}^{2}}{(x+1)(x-1)}$-$\frac{x}{x-1}$
=$\frac{x+1}{x-1}$-$\frac{x}{x-1}$
=$\frac{1}{x-1}$
(2)∵$\left\{\begin{array}{l}{x-1≥0}\\{x-3<0}\end{array}\right.$
∴$\left\{\begin{array}{l}{x≥1}\\{x<3}\end{array}\right.$
∴1≤x<3,
∵x为整数,
∴x=1或x=2,
①当x=1时,
∵x-1≠0,
∴A=$\frac{1}{x-1}$中x≠1,
∴当x=1时,A=$\frac{1}{x-1}$无意义.
②当x=2时,
A=$\frac{1}{x-1}$=$\frac{1}{2-1}=1$.
点评 (1)此题主要考查了分式的化简求值,注意化简时不能跨度太大,而缺少必要的步骤.
(2)此题还考查了求一元一次不等式组的整数解问题,要熟练掌握,解决此类问题的关键在于正确解得不等式组或不等式的解集,然后再根据题目中对于解集的限制得到下一步所需要的条件,再根据得到的条件求得不等式组的整数解即可.

练习册系列答案
相关题目
19.某服装经销商发现某款新型运动服市场需求量较大,经过市场调查发现年销售量y(件)与销售单价x(元)之间存在如图1所示的一次函数关系,而该服装的进价z(元)与销售量y(件)之间的关系如下表所示.已知每年支付员工工资和场地租金等费用总计2万元.
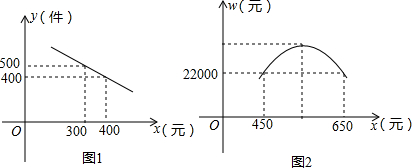
(1)求y关于x的函数关系式;
(2)写出该经销商经销这种服装的年获利W(元)关于销售单价x(元)的函数关系式.当销售单价x为何值时,年获利最大?并求出这个最大值;
(3)若经销商希望该服装一年的销售获利不低于2.2万元,请你根据图2象帮助确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
| 销售数量y(件) | … | 300 | 400 | 500 | 600 | … |
| 进货价格z(元) | … | 340 | 320 | 300 | 280 | … |

(1)求y关于x的函数关系式;
(2)写出该经销商经销这种服装的年获利W(元)关于销售单价x(元)的函数关系式.当销售单价x为何值时,年获利最大?并求出这个最大值;
(3)若经销商希望该服装一年的销售获利不低于2.2万元,请你根据图2象帮助确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
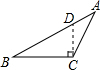
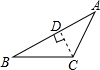
14.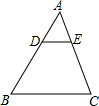 如图,在△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中正确的是( )
 如图,在△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中正确的是( )| A. | $\frac{AE}{AC}$=$\frac{1}{2}$ | B. | $\frac{DE}{BC}$=$\frac{1}{2}$ | ||
| C. | $\frac{△ADE的周长}{△ABC的周长}$=$\frac{1}{3}$ | D. | $\frac{△ADE的面积}{△ABC的面积}$=$\frac{1}{3}$ |



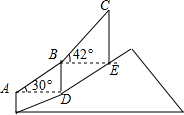 如图,登山缆车从点A出发,途经点B后到达终点C,其中AB段与BC段的运行路程均为200m,且AB段的运行路线与水平面的夹角为30°,BC段的运行路线与水平面的夹角为42°,求缆车从点A运行到点C的垂直上升的距离.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
如图,登山缆车从点A出发,途经点B后到达终点C,其中AB段与BC段的运行路程均为200m,且AB段的运行路线与水平面的夹角为30°,BC段的运行路线与水平面的夹角为42°,求缆车从点A运行到点C的垂直上升的距离.(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90) 将图中所示的图案以圆心为中心,旋转180°后得到的图案是( )
将图中所示的图案以圆心为中心,旋转180°后得到的图案是( )


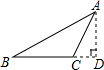
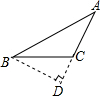
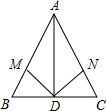 如图,在△ABC中,已知AB=AC,AD平分∠BAC,点M,N分别在AB,AC边上,AM=2MB,AN=2NC.求证:DM=DN.
如图,在△ABC中,已知AB=AC,AD平分∠BAC,点M,N分别在AB,AC边上,AM=2MB,AN=2NC.求证:DM=DN.