题目内容
11.已知二次函数y=x2-2x-3.(1)把函数化为y=a(x+m)2+k的形式,并指出抛物线的开口方向、顶点坐标和对称轴;
(2)画出这个函数的图象;
(3)根据图象回答:x取何值时,y随x的增大而增大?x取何值时,y随x的增大而减小?
(4)根据图象回答:函数y有最大值还是最小值?最大(小)值是多少?
(5)根据图象回答:x取何值时,y>0,y=0,y<0?
分析 (1)利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式;当a>0时,抛物线开口向上,它的对称轴是x=h,顶点坐标是(h,k);
(2)再求得抛物线与x轴的交点坐标和y轴的交点坐标,再画图即可;
(3)根据图象求得即可.
(4)根据图象求得即可;
(5)根据图象求得即可.
解答 解:(1)y=x2-2x-3
=(x2-2x+1)-4
=(x-1)2-4
即y=(x-1)2-4,
a=1>0,抛物线的开口向上,
顶点坐标为(1,-4),对称轴为x=1;
(2)令y=0,得x2-2x-3=0,得(x-1)2=4,所以x=±2,
令x=0,得y=-3,抛物线与y轴的交点坐标(0,-3);
画图象得:
(3)由图象得出:当x>1时,y随x的增大而增大;当x<1时,y随x的增大而减小.
(4)由图象可知函数y有最小值,最小值为-4;
(5)由图象可知:当x<-1或x>3时,y>0;当x=-1或x=3时,y=0;当-1<x<3时,y<0;
点评 本题考查了二次函数的三种形式、二次函数的图象以及二次函数的性质,注意画图的五步:开口方向,对称轴及顶点坐标,与x轴的交点坐标和y轴的交点坐标.

练习册系列答案
相关题目
14.某村原有林地108公顷,旱地54公顷,为保护环境,需把一部分旱地改造为林地,使旱地面积占林地面积的20%.设把x公顷旱地改为林地,则可列方程( )
| A. | 54-x=20%×108 | B. | 54-x=20%(108+x) | C. | 54+x=20%×162 | D. | 108-x=20%(54+x) |
2.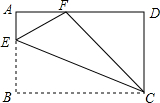 如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为( )
如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为( )
 如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为( )
如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为( )| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{4}{5}$ |
19.某服装经销商发现某款新型运动服市场需求量较大,经过市场调查发现年销售量y(件)与销售单价x(元)之间存在如图1所示的一次函数关系,而该服装的进价z(元)与销售量y(件)之间的关系如下表所示.已知每年支付员工工资和场地租金等费用总计2万元.
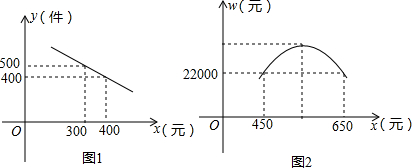
(1)求y关于x的函数关系式;
(2)写出该经销商经销这种服装的年获利W(元)关于销售单价x(元)的函数关系式.当销售单价x为何值时,年获利最大?并求出这个最大值;
(3)若经销商希望该服装一年的销售获利不低于2.2万元,请你根据图2象帮助确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
| 销售数量y(件) | … | 300 | 400 | 500 | 600 | … |
| 进货价格z(元) | … | 340 | 320 | 300 | 280 | … |

(1)求y关于x的函数关系式;
(2)写出该经销商经销这种服装的年获利W(元)关于销售单价x(元)的函数关系式.当销售单价x为何值时,年获利最大?并求出这个最大值;
(3)若经销商希望该服装一年的销售获利不低于2.2万元,请你根据图2象帮助确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
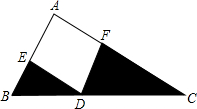 如图,在直角三角形ABC中,∠A=90°,点D在斜边BC上,点E,F分别在直角边AB,AC上,且BD=5,CD=9,四边形AEDF是正方形,则阴影部分的面积为$\frac{45}{2}$.
如图,在直角三角形ABC中,∠A=90°,点D在斜边BC上,点E,F分别在直角边AB,AC上,且BD=5,CD=9,四边形AEDF是正方形,则阴影部分的面积为$\frac{45}{2}$.



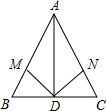 如图,在△ABC中,已知AB=AC,AD平分∠BAC,点M,N分别在AB,AC边上,AM=2MB,AN=2NC.求证:DM=DN.
如图,在△ABC中,已知AB=AC,AD平分∠BAC,点M,N分别在AB,AC边上,AM=2MB,AN=2NC.求证:DM=DN.