题目内容
3个连续偶数的和为36,则它们的积为( )
| A、1868 | B、1680 |
| C、1200 | D、998 |
考点:一元一次方程的应用
专题:数字问题
分析:设三个连续偶数中,中间的一个数为x,则较小的数为x-2,较大的数为x+2,根据这三个数的和为36建立方程求出这三个数就可以求出积.
解答:解:三个连续偶数中,中间的一个数为x,则较小的数为x-2,较大的数为x+2,由题意,得
x+x-2+x+2=36,
解得:x=12,
∴较小的数为10,较大的数为14,
∴它们的积为:10×12×14=1680.
故选B.
x+x-2+x+2=36,
解得:x=12,
∴较小的数为10,较大的数为14,
∴它们的积为:10×12×14=1680.
故选B.
点评:本题考查了连续偶数的性质的运用,列一元一次方程解实际问题的运用,一元一次方程的解法的运用,解答时建立一元一次方程求出三个连续的偶数是关键.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
下列条件能判断两个三角形全等的是( )
①两角及一边对应相等;
②两边及其夹角对应相等;
③两边及一边所对的角对应相等;
④两角及其夹边对应相等.
①两角及一边对应相等;
②两边及其夹角对应相等;
③两边及一边所对的角对应相等;
④两角及其夹边对应相等.
| A、①③ | B、②④ |
| C、②③④ | D、①②④ |
已知
xm+nym-n与-9x7-my1+n的和是单项式,则m,n的值分别是( )
| 3 |
| 5 |
| A、m=-1,n=-7 | ||||
| B、m=3,n=1 | ||||
C、m=
| ||||
D、m=
|
已知a的平方根是±8,则a的立方根是( )
| A、2 | B、4 | C、±2 | D、±4 |
 如图,抛物线y=x2沿直线y=x向上平移
如图,抛物线y=x2沿直线y=x向上平移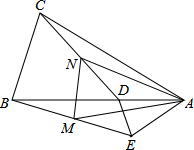 如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点,下列结论:
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点,下列结论: 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中不正确的有( )个.
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中不正确的有( )个. 已知:如图,BC=BE,AB=FB,∠1=∠2,求证:∠C=∠BEF.
已知:如图,BC=BE,AB=FB,∠1=∠2,求证:∠C=∠BEF.